تعداد فایل‌ها: ۳ فایل

توضیحات:

در این پروژه، یک مثال برنامه ریزی ریاضی غیر خطی با شرایط فازی را ساخته و با رویکرد برش الفا مقدار بهینه تابع هدف را می‌سازیم. برای حل مدل‌های ریاضی از نرم افزار GAMS استفاده کرده‌ایم.

۱- تعاریف مقدماتی

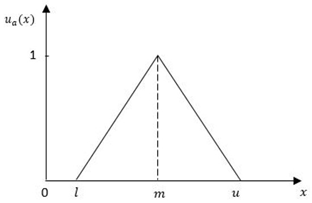
یک عدد فازی مثلثی $ \tilde{A} $ (همانطور که در شکل 1 نشان داده شده است) به عنوان یک عدد سه تایی$ ( l , m , n ) $ تعریف می شود و تابع عضویت آن به صورت زیر است:

$ \mu_A (x)  = \begin{cases} 0 & x\le 1 \\ \frac{x-l}{m-l} & l \le x \le m  \\ \frac{u-x}{u-m} & m \le x \le u  \\ 0 & x \ge u \end{cases} $

تعریف 2 (برش آلفا). برش آلفا برای مجموعه فازی $ \tilde{A} (A_{\alpha}) $ مجموعه خاصی است که شامل مجموعه‌ای از عناصر است که درجه عضویت آن‌ها  برابر یا بیشتر از مقدار آلفا است

$ A_{\alpha} = \{ x \in X \left| \mu_{\tilde{A}} (x) \ge \alpha \right. \} $

که در آن $ \tilde{A} = ( 1,m,n ) $ به عنوان یک عدد فازی مثلثی منظور می‌شود که برش آلفای آن به صورت زیر است:

$ A_{\alpha} = [l + \alpha (m-l), u - \alpha (u-m) ] $

در ادامه، تعاریف جدیدی برای مقایسه اعداد فازی مثلثی بر اساس اعداد فازی مثلثی اصلاح شده (TFN) ارائه شده است.

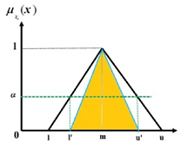
تعریف 3 (اعداد فازی مثلثی اصلاح شده (MTFN)). فرض کنید $ \tilde{A} = ( 1,m,n ) $ را می توان به عنوان یک عدد فازی مثلثی توصیف کرد، عدد فازی مثلثی اصلاح شده (همانطور که در شکل 2 نشان داده شده است) به صورت زیر تعریف می شود:

$ \mu_{A_{\alpha}} (x)  = \begin{cases} \frac{x-l^{\prime}}{m-l^{\prime}} & l^{\prime} \le x \le m \\ 1 & x = m  \\ \frac{u^{\prime}-x}{u^{\prime}-m} & m \le x \le u^{\prime}   \end{cases}, $

که در آن $ l , m ,n $ به ترتیب نشان دهنده مقدار پایین، مودال و بالای پشتیبان  $ \tilde{A} $ و همگی اعداد کریسپ هستند $ ( -\infty < l  \le m \le u < + \infty ) $ . علاوه بر این ، $ l^{\prime} $ و $ u^{\prime} $ ، به ترتیب، مقادیر پایین و بالایی اعداد فازی مثلثی اصلاح شده را نشان می‌دهند.

اطلاعات کامل رو در فایل ببینید...

این مجموعه شامل فایل pdf توضیحات (تایپ شده) و فایل برنامه نرم‌افراز گمز (Gams) می‌باشد که در یک فایل فشرده تقدیم شما می‌گردد.