استقلال خطی

در این درس به بیان تعاریف و مفاهیم مربوط به استقلال خطی توابع می پردازیم.  به تعاریف زیر توجه کنید:

 

[tabs ] [tab_item title=" تعریف وابسته خطی" ]

تعريف 7.3: دو تابع نامستقل خطي (وابسته خطي):

دو تابع 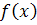و 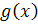را نامستقل خطي ( وابسته خطي ) مي گوييم هرگاه عدد ثابتي مانند 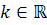وجود داشته باشد به طوري که .

 

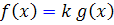به بيان ساده تر ، دو تابع را وابسته خطي مي گوييم اگر يکي مضرب ثابتي از ديگري باشد.

[/tab_item] [tab_item title=" تعریف مستقل خطی" ]

تعريف 8.3: دوتابع مستقل خطي:

دو تابع f و g که وابسته خطي نيستند را مستقل خطي مي ناميم.

[/tab_item] [tab_item title=" مثال" ]

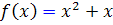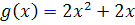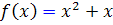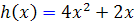مثال 1.3: دو تابع و وابسته خطي اند و توابع و مستقل خطي اند.

[/tab_item] [tab_item title=" تعمیم " ]

مستقل بودن دو تابع و وابستگي را مي توان به بازه ها نيز محدود کرد. همچنين اين ويژگي ها را مي توان به بيش از دو تابع نيز گسترش داد. تعريف زير اين امکان ها را فراهم مي کند :

تعريف 9.3: تعميم توابع وابسته و مستقل خطي :

فرض کنيد توابع غير متحد با صفر ( 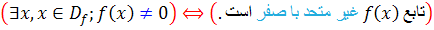) 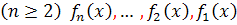بر بازه ي I تعريف شده باشند. اگر ثابت هاي 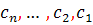که حداقل يکي از آن ها مخالف صفر است؛ طوري وجود داشته باشند که به ازاي هر x از بازه ي I داشته باشيم :

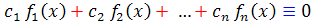
آنگاه مي گوييم اين توابع بر بازه ي I ، نامستقل خطي اند.

همچنين اگر براي توابع فوق ، چنين 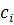هايي موجد نباشد، توابع را مستقل خطي مي ناميم.

[/tab_item] [/tabs]