Midterm of Advanced Algebra Dr S.keyvanfar1386/9/18
Advanced Algebra
Midterm MSc. Exam
Department of MathematicsFerdowsiUniversity of Mashhad
1386/9/18
Dr S.keyvanfar
1. LetX be a nonempty set and F=F(X) is the set of all reduced words on X. show that F is a group under the binary opration defined in your course.
2. Prove that every unitarymodule A over a Ring R with identity may be embedded in an injective R-module .
3. Does there exist a free object in the category of all unitary left R-modules, when R is a Ring with identity ?Prove your claim and if your answeris positive , give its enplicit structure.
4. Show that the additive group 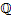 is not finitely generated.
is not finitely generated.
5. What are the elementary divisors ofthe group
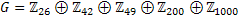
6. Prove in details that every divisible abelian group is a direct sum of copies of the vationals 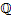 and copies of
and copies of 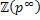 .
.
- بازدید: 28581