پايان ترم توابع مختلط دكتر صبورملكي 30/3/85

نام آزمون : پايان ترم توابع مختلط

تاريخ برگزاري : 30/3/1385

نام استاد :دكتر صبور ملكي

دانشگاه : فردوسي مشهد

دانشكده : علوم رياضي و آمار

1. ثابت كنيد هر دنباله يهمگرا از اعداد مختلط كراندار است.

2. تابع f در قرص باز 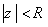تحليلي است. به ازاي هر z در اين قرص تابع f داراي نمايش به صورت سري زير است :

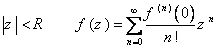
پس از اثبات حكم بالا تابع sinh z را به صورت يك سري تواني نوشته و حزه ي همگرايي اش را مشخص كنيد.

3. بسط لوران تابع 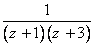را در حوزه ي 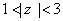بدست آوريد.

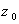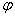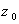4. قطب مرتبه m تابع f را تعريف كنيد. اگر قطب مرتبه ي m تابع f باشد، آنگاه نشان دهيد تابع در تحليلي است :

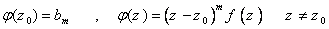
سپس مانده ي تابع f را در 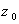بدست آورده انتگرال زير را محاسبه نمائيد.

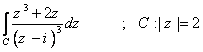
5. مقدار اصلي كوشي انتگرال 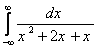را بدست آوريد.

6. الف : نشان دهيد تبديل 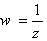خطوط و دواير در صفحه ي zها را به خطوط و دواير در صفحه ي wها مي برد. تصوير هذلولي 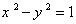را تحت اين تبديل مشخص كنيد.

ب : تبديل دو خطي اي را بيابيد كه نقاط متمايز 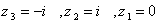را به ترتيب به 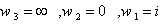مي برد. اين تبديل محور yها را به چه منحني تبديل مي كند.