پایانترم توابع مختلط دکتر فتوحی دانشگاه شریف 13930322
نام آزمون: پایانترم توابع مختلط
دانشگاه: صنعتی شریف
تاریخ برگزاری آزمون: 13930322
استاد : دکتر فتوحی
وقت امتحان: 3 ساعت
دانلود فایل PDF این نمونه سوال
-
فرض کنید ناحیه
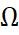 یک مجموعه باز باشد که شامل بستار دیسک
یک مجموعه باز باشد که شامل بستار دیسک 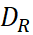 است. همچنین تابع هلومورف f روی دایره
است. همچنین تابع هلومورف f روی دایره 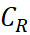 مخالف صفر است و
مخالف صفر است و 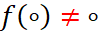 . اگر
. اگر 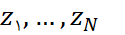 ریشه های تابع f با احتساب تکرر درون دیسک
ریشه های تابع f با احتساب تکرر درون دیسک 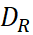 باشد، آنگاه رابطه زیر را اثبات کنید:
باشد، آنگاه رابطه زیر را اثبات کنید: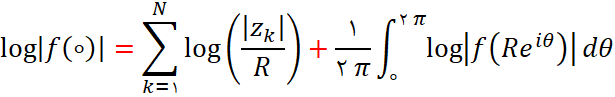
-
اگر تابع
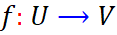 هلومورف و یک به یک باشد، ثابت کنید
هلومورف و یک به یک باشد، ثابت کنید 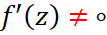 برای هر
برای هر 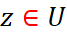 و وارون تابع f نیز یک تابع هلومورف است.
و وارون تابع f نیز یک تابع هلومورف است. -
فرض کنید
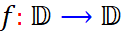 نگاشت هلومورف باشد که
نگاشت هلومورف باشد که 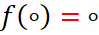 و
و 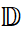 دیسک واحد به مرکز مبدأ است. ثابت کنید
دیسک واحد به مرکز مبدأ است. ثابت کنید 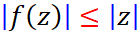 برای هر
برای هر 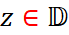 و اگر تساوی برای نقطه ای به غیر از مبدأ اتفاق بیافتد آنگاه تابع f یک دوران است.
و اگر تساوی برای نقطه ای به غیر از مبدأ اتفاق بیافتد آنگاه تابع f یک دوران است. -
اگر
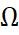 ناحیه باز و همبند باشد و
ناحیه باز و همبند باشد و 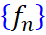 دنباله توابع هلومورف و یک به یک روی
دنباله توابع هلومورف و یک به یک روی 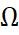 که روی زیرمجموعه های فشرده به طور یکنواخت به تابع f همگرا است. نشان دهید f یک به یک یا تابع ثابت است.
که روی زیرمجموعه های فشرده به طور یکنواخت به تابع f همگرا است. نشان دهید f یک به یک یا تابع ثابت است. -
رابطه زیر را اثبات کنید:
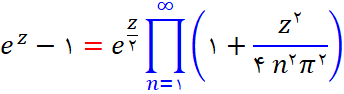
-
ثابت کنید هر تابع تام و یک به یک به صورت
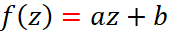 است.
است. -
الف- یک نگاشت همدیس از ناحیه زیر به نیم صفحه بیابید.
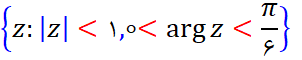
ب- یک جواب برای معادله
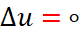 در این ناحیه پیدا کنید که در شرایط مرزی زیر صدق می کند.
در این ناحیه پیدا کنید که در شرایط مرزی زیر صدق می کند.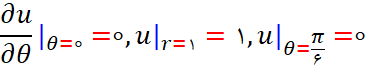
دانلود فایل PDF این نمونه سوال
موفق باشید
سایر نمونه سوالات توابع مختلط
لیست نمونه سوالات دانشگاه شریف
نمونه سوال امتحانی, 1393, نمونه سوالات دانشگاهی, دانشگاه صنعتی شریف, pdf, نمونه سوالات دانشگاه صنعتی شریف, دکتر مرتضی فتوحی, نمونه سوالات توابع مختلط
- بازدید: 5675