آزمون پایانی مبانی ریاضیات نیمسال اول 86-85 دکتر حامد

به نام خدا

اللهم صل علي محمد و آل محمد

نام آزمون: پايان ترم مباني رياضيات

نام استاد: دکتر حامد

تاريخ برگزاري: نيمسال اول 86-85

دانشگاه: فردوسي مشهد

دانشکده: علوم رياضي

1. ساخت مجموعه اعداد طبيعي را به صورت يک دستگاه اصل موضوعي شرح دهيد.

2. خاصيت جابجايي عمل جمع در مجموعه ي اعداد طبيعي را ثابت کنيد.

3. نشان دهيد هر مجموعه ي نامتناهي شامل يک زيرمجموعه ي شماراي نامتناهي است.

4. نشان دهيد مجموعه ي A ناشماراست اگروتنها اگر 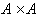ناشمارا باشد.

5. قضيه ي شرودر- برنشتاين را بيان و اثبات کنيد.

6. مجموعه ي اعداد اصلي ترامتناهي، متناهي است يا نامتناهي؟ چرا؟

7. مقدار c+c را به دست آوريد.

8. نشان دهيد.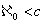

9. نشان دهيد اصل انتخاب، از اصل خوشترتيبي نتيجه مي شود.

10. فرض کنيد X يک مجموعه و 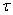مجموعه اي از زيرمجموعه هاي X است. مي گوييم 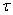داراي مشخصه ي متناهي است، هر گاه 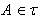اگروتنها اگر هر زير مجموعه ي متناهي A عضو 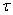باشد. ثابت کنيد که اگر 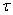مشخصه ي متناهي داشته باشد، آن گاه 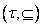عضو ماکسيمال دارد.

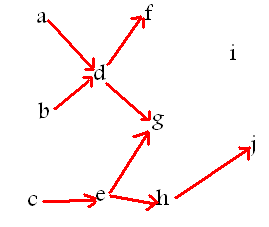
11. نمودار زير يک مجموعه ي مرتب جزئي را نشان مي دهد. همه ي عناصر مينيمم، ماکسيمم، مينيمال و ماکسيمال را مشخص کرده و تمام زنجيره هاي ماکسيمال را نيز بنويسيد.