Real Analysis 1386/09/06 Dr. H.R.E.vishki
Exam : Real Analysis
Date : 1386/09/06
Pro : Dr. H.R.E.vishki
Uni : Ferdowsi of Mashad
1. Define ![]() by
by
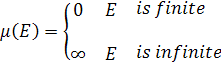
show that ![]() is finitely additive but it is not a measure on
is finitely additive but it is not a measure on ![]() .
.
2. Let ![]() be a complete measure on X :
be a complete measure on X :
i ) if ![]() are two functions such that f=ga.e , then show that the measurability off is equivalent to that of g.
are two functions such that f=ga.e , then show that the measurability off is equivalent to that of g.
ii ) Let ![]() a.e, show that if
a.e, show that if![]() is measurable for all
is measurable for all ![]() then so is f.
then so is f.
3. i ) State and prove Dominated Convergence Theorem.
ii ) Let![]() be a sequence of bounded measurable functions such that
be a sequence of bounded measurable functions such that ![]() on X , show that if
on X , show that if ![]() Then
Then
![]()
Through an example show that the hypothesis " ![]() " is essential.
" is essential.
4. i ) Show that ![]() is Banach.
is Banach.
ii ) Show that ![]() and
and ![]() for every finite measure
for every finite measure ![]() . Is the same inclusion true when
. Is the same inclusion true when ![]() is infinite . Prove yours claim.
is infinite . Prove yours claim.
- بازدید: 27487