معادله دیفرانسیل همگن شدنی مرتبه اول
به نام خدا
الهم صل علی محمد و آل محمد
دسته اي از معادلات ديفرانسيل به ظاهر همگن نيستند، اما با تغيير متغير هاي مناسب ، مي توان آن ها را به معادلات همگن تبديل نمود.
اين معادلات اين گونه اند:
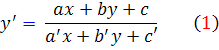
که در آن 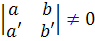 . ( شما با اين شکل از معادلات ، در قسمت معادلات جداشدني آشنا شده ايد. در آنجا
. ( شما با اين شکل از معادلات ، در قسمت معادلات جداشدني آشنا شده ايد. در آنجا 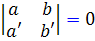 ).
).
دقت داريم که a x + b y + c = 0 و a' x + b' y + c' = 0 ، با شرط 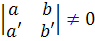 ، معادلات خطوط متقاطع در صفحه اند. از همين نکته براي به دست آوردن تغيير متغير استفاده استفاده مي کنيم.
، معادلات خطوط متقاطع در صفحه اند. از همين نکته براي به دست آوردن تغيير متغير استفاده استفاده مي کنيم.
ابتدا محل تقاطع اين دو خط را مي يابيم . اگر نقطه ي 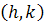 ، نقطه ي برخورد دو خط باشد، کافي است تغيير متغير هاي
، نقطه ي برخورد دو خط باشد، کافي است تغيير متغير هاي 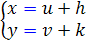 را انتخاب کنيم. در اين صورت
را انتخاب کنيم. در اين صورت 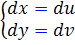 .
.
با مثال زير با ادامه ي روش آشنا مي شويم :
[/tab_item] [tab_item title="مثال"]مثال 10.2: معادله ي 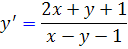 را حل کنيد.
را حل کنيد.
حل: توجه داريم که 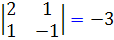 و دستگاه
و دستگاه 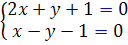 داراي جواب
داراي جواب 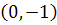 است. پس قرار مي دهيم:
است. پس قرار مي دهيم:
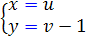
و داريم:
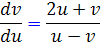
اکنون اين معادله را به معادله ي همگن تبديل مي کنيم:
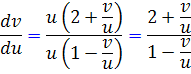
که با تغيير متغير 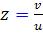 خواهيم داشت:
خواهيم داشت:
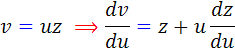
بنابراين:
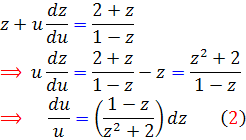
که معادله ي 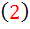 ، يک معادله ي جداپذير استاندارد است و چواب عمومي آن اين گونه است:
، يک معادله ي جداپذير استاندارد است و چواب عمومي آن اين گونه است:
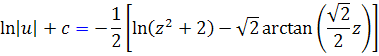
اکنون مقدار 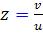 را قرار مي دهيم:
را قرار مي دهيم:
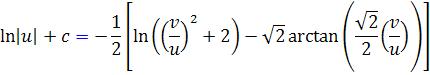
و اگر قرار دهيم 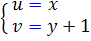 خواهيم داشت:
خواهيم داشت:
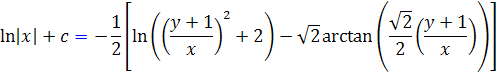
که اين جواب عمومي معادله ي داده شده است.
به اين ترتيب فراگرفتيم که چگونه يک معادله به صورت 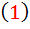 را به معادله ي همگن تبديل کنيم.
را به معادله ي همگن تبديل کنيم.
- بازدید: 17390