مثالها و تستهایی در عامل انتگرال ساز
به نام خدا
الهم صل علي محمد و آل محمد
مثال هاي زير را دنبال کنيد تا با چگونگي يافتن عامل انتگرال ساز و استفاده از آن در حل معادله ديفرانسيل کامل شدني بيشتر آشنا شويد.
مثال 15.2: معادله ديفرانسيل 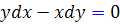 را حل کنيد.
را حل کنيد.
حل: دقت داريم که 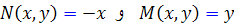 . پس
. پس 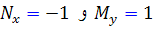 که نشان مي دهد معادله کامل نيست.
که نشان مي دهد معادله کامل نيست.
اکنون به جستجوي عامل انتگرال سازي مي پردازيم که معادله ي داده شده را به معادله ي کامل تبديل کند.
تساوي 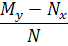 را تشکيل مي دهيم. داريم:
را تشکيل مي دهيم. داريم:
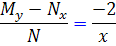
مشاهده مي کنيد که حاصل اين کسر ، تابعي تک متغيره از x است . آن را 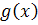 مي ناميم . پس
مي ناميم . پس
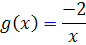
بنابراين بايستي از فرمول حالت اول ، عامل انتگرال ساز را بيابيم :
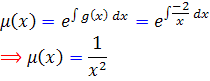
اگر 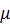 را در معادله ي اصلي ضرب کنيم ، يک معادله ي کامل به دست مي آيد :
را در معادله ي اصلي ضرب کنيم ، يک معادله ي کامل به دست مي آيد :
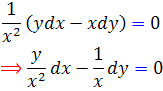
اکنون جواب اين معادله را مي يابيم :
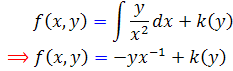
اما
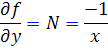
. پس
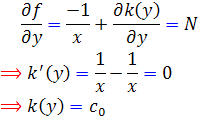
بنابراين تابع 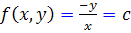 جواب عمومي معادله است.
جواب عمومي معادله است.
این مثال از تست هاي کنکور کارشناسي ارشد انتخاب شده است . اين تست در سال 1382 در آزمون کارشناسي ارشد مهندسي مواد ورودي دانشگاه آزاد اسلامي آمده است .
مثال 16.2: کدام يک از عبارات زير يک عامل انتگرال ساز معادله ي 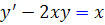 است ؟
است ؟
1. 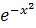
2. 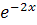
3. 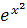
4. 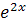
حل:
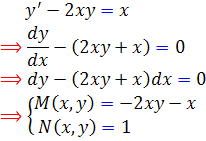
اکنون دنبال عامل انتگرال ساز مي گرديم. چون 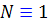 ، پس بهتر است از حالت اول استفاده کنيم :
، پس بهتر است از حالت اول استفاده کنيم :
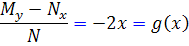
پس عامل انتگرال ساز به صورت زير خواهد بود :
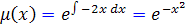
بنابراين گزينه ي 1 پاسخ صحيح خواهد بود.
[/tab_item] [tab_item title="مثال سوم" ]مثال 17.2: معادله ديفرانسيل زير را با به دست آوردن عامل انتگرال ساز حل کنيد :
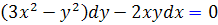
حل: با توجه به اينکه معادله کامل نيست ، در پي عامل انتگرال ساز هستيم :
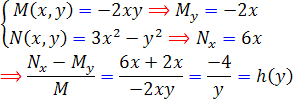
بنابراين با توجه به حالت دوم ، عامل انتگرال ساز به صورت زير است :
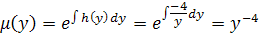
اکنون به حل معادله مي پردازيم. عامل انتگرال ساز را در معادله ضرب مي کنيم ، معادله ي جديد کامل است و آن را حل مي کنيم :
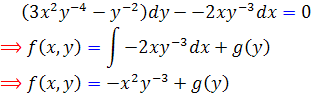
اما با توجه به 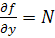 داريم:
داريم:
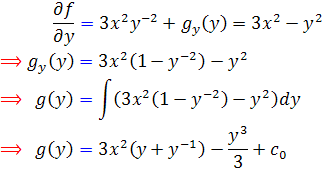
بنابراين جواب عمومي معادله به صورت زير خواهد بود :
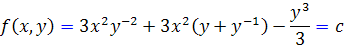
- بازدید: 21845