معادله لاگرانژ: دسته سوم معادلات خطی شدنی
به نام خدا
الهم صل علی محمد و آل محمد
معادله لاگرانژ
هر معادله ديفرانسيل به صورت
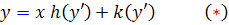
يک معادلهي لاگرانژ ناميده مي شود.
براي حل معادلات لاگرانژ ، از تغيير متغير 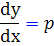 استفاده مي کنيم. بنابراين
استفاده مي کنيم. بنابراين
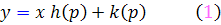
معادله ي لاگرانژ است.
در حالت خاصي که 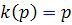 باشد، معادله ي لاگرانژ به معادله ي کلرو تبديل مي شود.
باشد، معادله ي لاگرانژ به معادله ي کلرو تبديل مي شود.
چگونگي حل يک معادله ي لاگرانژ :
با فرض اينکه 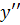 موجود باشد ، از معادله ي
موجود باشد ، از معادله ي ![]() نسبت به x مشتق مي گيريم :
نسبت به x مشتق مي گيريم :
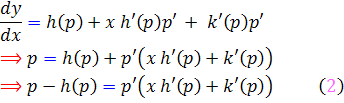
براي معادله ي ![]() دو حالت زير را در نظر مي گيريم :
دو حالت زير را در نظر مي گيريم :
حالت اول : به ازاي مقادير ِ ثابتي از p ، معادله ي 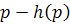 صفر است . مثلا ً اگر
صفر است . مثلا ً اگر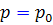 ، آنگاه
، آنگاه 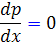 و در اين صورت
و در اين صورت 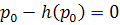 . پس دو طرف تساوي
. پس دو طرف تساوي ![]() صفر است.
صفر است.
براي به دست آوردن جواب متناظر ،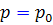 را در معادله ي
را در معادله ي ![]() قرار مي دهيم :
قرار مي دهيم :
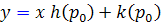
که اين معادله ، يک خط راست خواهد بود و جواب غير عادي معادله ي ![]() است زيرا جواب عمومي آن در حالت دوم به دست مي آيد.
است زيرا جواب عمومي آن در حالت دوم به دست مي آيد.
حالت دوم : در اين حالت فرض کنيم  . بنابراين معادله ي
. بنابراين معادله ي ![]() به صورت زير خواهد شد :
به صورت زير خواهد شد :
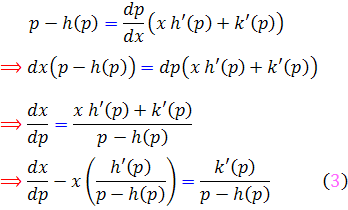
با دقت در معادله ي ![]() در مي يابيم يک معادله ي خطي است که در آن x تابعي از p است. با حل معادله ي
در مي يابيم يک معادله ي خطي است که در آن x تابعي از p است. با حل معادله ي ![]() ، تابعي مانند
، تابعي مانند 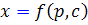 به دست مي آيد که آن را در معادله ي
به دست مي آيد که آن را در معادله ي ![]() قرار داده و تابع y را بر حسب x به دست مي آوريم. تابع به دست آمده جواب عمومي معادله ي لاگرانژ خواهد بود.
قرار داده و تابع y را بر حسب x به دست مي آوريم. تابع به دست آمده جواب عمومي معادله ي لاگرانژ خواهد بود.
به مثال زير دقت کنيد تا معادله ي لاگرانژ را بهتر درک کنيد و عملا ً با چگونگي حل يک معادله ي لاگرانژ آشنا شويد.
مثال 22.2 : معادله ي لاگرانژ 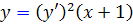 را حل کنيد .
را حل کنيد .
حل : قرار مي دهيم 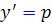 و از معادله نسبت به x مشتق مي گيريم :
و از معادله نسبت به x مشتق مي گيريم :
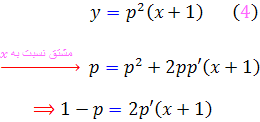
اکنون دو حالت داريم :
حالت اول: 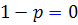 . پس p=1 و y = x + 1 جواب غير عادي معادله است.
. پس p=1 و y = x + 1 جواب غير عادي معادله است.
حالت دوم: 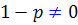 . پس :
. پس :
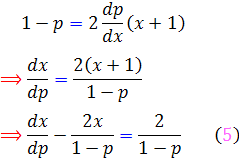
معادله ي ![]() يک معادله ي خطي مرتبه ي اول است . عامل انتگرال ساز را يافته و جواب عمومي
يک معادله ي خطي مرتبه ي اول است . عامل انتگرال ساز را يافته و جواب عمومي ![]() را مي يابيم :
را مي يابيم :
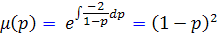
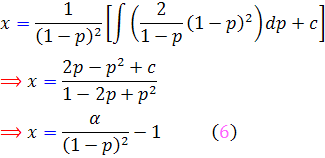
که 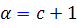 .
.
اکنون با توجه به تساوي هاي ![]() و
و ![]() ، جواب عمومي معادله ي اصلي به صورت زير خواهد بود :
، جواب عمومي معادله ي اصلي به صورت زير خواهد بود :
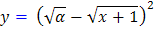
- بازدید: 34099