معادلات دیفرانسیل جداپذیر
به نام خدا
الـهم صل علی مـحمد و آل محـمد
ساده ترين شکل معادلات ديفرانسيل، معادلات جداپذير هستند. براي حل اين معادلات کافي است آن ها را به شکل استاندارد در آورده ، انتگرال بگيريم تا تابع مجهول به دست آيد.
معادله جداپذیر
شکل کلي يک معادله ديفرانسيل جداپذير اين گونه است:
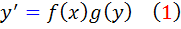
يا
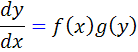
که در آن ها 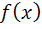 تابعي از x و
تابعي از x و 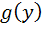 تابعي از y است.
تابعي از y است.
شکل استاندارد معادله ديفرانسيل جداپذیر نيز اين گونه است:
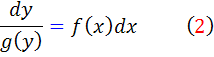
که در اين حالت ِ معادله، متغير هاي x و y ، از يکديگر جدا شده اند. يعني عبارات ِ شامل x در يک سمت علامت تساوي و عبارات شامل y در سمت ديگر آن آمده اند. به همين دليل است که اين معادلات را معادلات جداپذير مي گويند.
[tabs ] [tab_item title="روش حل" ]
روش حل معادلات جداپذیر
حل اين معادلات بسيار ساده است. کافي است از عبارات شامل x ، نسبت به x و از عبارات شامل y ، نسبت به y انتگرال بگيريم.
پس جواب عمومي معادله جداپذير استاندارد اين گونه است :
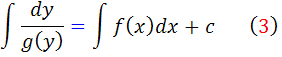
[/tab_item] [tab_item title="مثال 1" ]
مثال 1.2: معادله ي 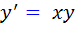 را حل کنيد.
را حل کنيد.
حل : ابتدا بررسي مي کنيم آيا اين معادله جداپذير است يا خير؟ اگر بتوانيم آن را به صورت استاندارد جداپذير در آوريم، معادله جداپذير است.
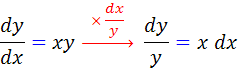
پس معادله جداپذير است و جواب عمومي آن به صورت زير است:
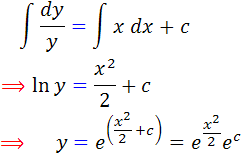
چون c عدد ثابت است پس 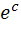 نيز ثابت است و مي توان آن را
نيز ثابت است و مي توان آن را 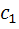 در نظر گرفت. پس
در نظر گرفت. پس 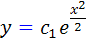 جواب عمومي معادله ي مورد نظر است.
جواب عمومي معادله ي مورد نظر است.
[/tab_item] [tab_item title="اثبات جواب عمومی"]
اثبات جواب عمومی :
براي اينکه ثابت کنيم عبارت  ، جواب عمومي عبارت
، جواب عمومي عبارت  است، اينگونه عمل مي کنيم:
است، اينگونه عمل مي کنيم:
با اختيار تابع 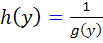 ، معادله ي
، معادله ي  به صورت زير در مي آيد:
به صورت زير در مي آيد:
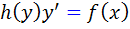
اکنون اگر 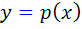 جواب معادله ديفرانسيل باشد داريم:
جواب معادله ديفرانسيل باشد داريم:
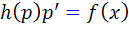
فرض کنيم q يک تابع اوليه براي h باشد يعني 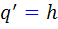 . در اين صورت داريم:
. در اين صورت داريم:
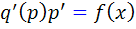
سمت چپ تساوي بالا، مشتق ِ تابع مرکب 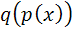 است . پس داريم:
است . پس داريم:
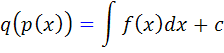
اما 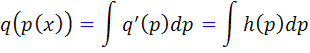 . پس
. پس
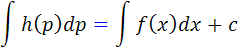
و
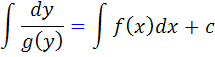
مثال 2.2: تحقيق کنيد آيا معادله ي 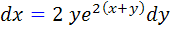 ، جداپذير است يا خير سپس در صورتي که معادله جداپذير است، جواب عمومي آن را بيابيد :
، جداپذير است يا خير سپس در صورتي که معادله جداپذير است، جواب عمومي آن را بيابيد :
حل :
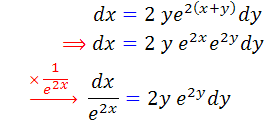
بنابراين معادله جداپذير است. اکنون کافي است از طرفين انتگرال بگيريم:
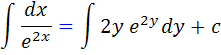
که با استفاده از تکنيک هاي انتگرال گيري، جواب انتگرال هاي بالا به صورت زير خواهد بود :
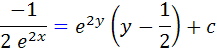
که اين جواب عمومي معادله ي داده شده است.
[/tab_item] [tab_item title="مثال 3" ]مثال 3.2: معادله ديفرانسيل جداپذير 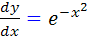 را حل کنيد.
را حل کنيد.
حل: شکل استاندارد اين معادله به صورت 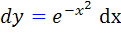 است. بنابراين جواب عمومي آن به صورت
است. بنابراين جواب عمومي آن به صورت 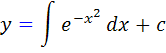 است. اما
است. اما 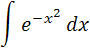 قابل محاسبه نيست و جواب عمومي به همين شکل باقي مي ماند.
قابل محاسبه نيست و جواب عمومي به همين شکل باقي مي ماند.
- بازدید: 20217