ترانهاده ماتریس و ویژگیهای آن
تعریف ترانهاده یک ماتریس: ماتریسی که از جابهجایی جای عناصر سطر و ستون یک ماتریس حاصل میشود را ترانهادهٔ آن ماتریس میگویند. یا به عبارت دیگر، فرض کنید $A=[a_{ij}]$ یک ماتریس از مرتبه $m\times n $ باشد، ماتریس از مرتبه $ n\times m$ که به وسیله تعویض سطرهای ماتریس A با ستونهای آن به دست میآید را ترانهاده ماتریس A میگویند. ترانهاده ماتریس A را با نمادهای $ A^{T} $ یا $ A^{t} $ نشان میدهیم. بصورت نمادهای ریاضی میتوان ترانهاده یک ماتریس را به گونه زیر بیان نمود:
$ A = [a_{ij}]_{m \times n} \rightarrow A^T = [a_{ji}]_{m \times n} $
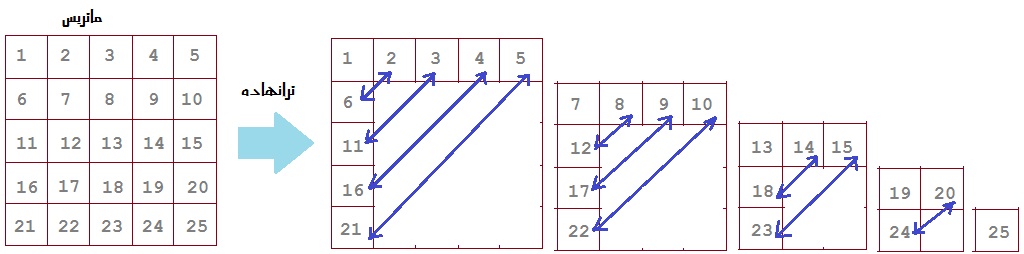
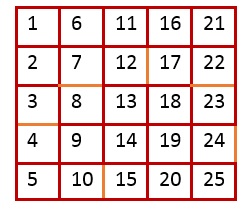
مثال ۱. فرض کنید که $ A = \begin{bmatrix}1 & 2 & 3 \\ 5 & 6 & 7 \end{bmatrix} $ باشد. در اینصورت ترانهاده این ماتریس به صورت زیر خواهد شد:
$ A^{T} = \begin{bmatrix}1 & 5 \\ 2 & 6 \\ 3 & 7 \end{bmatrix} $
مثال ۲. فرض کنید $ A = \begin{bmatrix}5 & 6 \\ 7 & 8 \end{bmatrix} $ باشد، در این صورت $ A^{T} = \begin{bmatrix}5 & 7 \\ 6 & 8 \end{bmatrix} $ خواهد بود. مشاهده میشود که در ترانهاده ماتریسهای مربعی جای عناصر بر روی قطر اصلی در ماتریس ترانهاده با ماتریس اولیه یکی است.
درباره ماتریس ترانهاده ویژگیهای زیر را داریم:
ویژگی ۱. .$ (A^{T})^{T} = A $ در واقع این موضوع بیان میکند که ترانهاده، ترانهاده یک ماتریس با خود آن ماتریس برابر خواهد شد.
مثال۳. $ A = \begin{bmatrix}1 & 2 & 3 \\ 5 & 6 & 7 \end{bmatrix} $ در این صورت $ A^T= \begin{bmatrix}1 & 5 \\ 2 & 6 \\ 3 & 7 \end{bmatrix} $ و $ (A^{T})^{T} = \begin{bmatrix}1 & 2 & 3 \\ 5 & 6 & 7 \end{bmatrix} $ خواهد بود.
ویژگی 2. $ (A+B)^{T} = A^{T} + B^{T} $. این موضوع بیان میکند که ترانهاده خاصیت پخش شدن را دارد.
مثال ۴. $ A = \begin{bmatrix}5 & 6 \\ 7 & 8 \end{bmatrix} $ و $ B = \begin{bmatrix}8 & 9 \\ 10 & 11 \end{bmatrix} $ در این صورت
$A^T =\begin{bmatrix}5 & 7\\ 6 & 8\end{bmatrix}$
$B^T = \begin{bmatrix} 8 & 10\\ 9 & 11 \end{bmatrix}$
و داریم:
$ (A+B) = \begin{bmatrix}5 + 8 & 9 + 6 \\ 10 + 7 & 8 +11 \end{bmatrix} = \begin{bmatrix}13 & 15 \\ 17 & 19 \end{bmatrix}$
$(A+B)^T= \begin{bmatrix}13 & 17 \\ 15 & 19 \end{bmatrix} $
از طرفی $ A^{T} + B^T= \begin{bmatrix}13 & 17 \\ 11 & 19 \end{bmatrix} $ خواهد بود.
ویژگی 3. $ (AB)^{T} = B^{T} A^{T} $.
مثال ۵. $ A = \begin{bmatrix}1 & 5 \\ 0 & 2 \end{bmatrix} $ و $ B = \begin{bmatrix}1 & 0 \\ 0 & 2 \end{bmatrix} $ باشد. در اینصورت
$AB=\begin{bmatrix}1 & 10\\ 0 & 4 \end{bmatrix}$
$(AB)^T= \begin{bmatrix}1 & 0\\ 10 & 4 \end{bmatrix}$
و
$B^T A^T =\begin{bmatrix}1 & 0\\ 0 & 2 \end{bmatrix} \begin{bmatrix} 1& 0\\ 0 & 2 \end{bmatrix} =\begin{bmatrix} 1&0\\ 10&4\end{bmatrix}$
ویژگی 4. ماتربس مربعی A وارون پذیر است اگر و فقط اگر $ A^T $ وارون پذیر باشد.
زماني كه ماتربس A وارون پذير است لذا ماتربس Bاي موجود است به قسمي كه داريم $AB=I$ است. با گرفتن ترانهاده از آن خواهيم داشت:
$ (AB)^T = I \rightarrow B^T A^T = I $
پس در نتيجه $A^T$ وارون پذير است. برای زمانی که $A^T$ وارون پذیر است نیز به صورت مشابه عمل کنید.
ویژگی 5. اگر c یک اسکالر باشد. داریم:
$(cA)^T = cA^T$
مثال ۶. مفروض است $ A = \begin{bmatrix}1 & 5 \\ 7 & 2 \end{bmatrix} $ و c = 5 .
$ \Longrightarrow A ^ {T} = \begin{bmatrix}1 & 7 \\ 5 & 2 \end{bmatrix} , cA = \begin{bmatrix}5 & 25 \\ 35 & 10 \end{bmatrix} \Longrightarrow (cA)^{T} = cA ^ {T} = \begin{bmatrix}5 & 35 \\ 25 & 10 \end{bmatrix} $
تمرین ۱. ترانهاده ماتریسهای زیر را به دست آورید.
۱. $A=\begin{bmatrix}5 & 25 &0\\ 35 & 10&1 \end{bmatrix} $
۲. $A=\begin{bmatrix} 1 & 2 \\ 3 & 0 \end{bmatrix}$ , $B=\begin{bmatrix} 0 & 1 \\ 5 & x \end{bmatrix}$ ⇒ $(AB)^T$
ماتریس, ماتریس مربعی, ترانهاده ماتریس
- بازدید: 34015