سری مک‌لورن

سری مک‌لورن ( Maclaurin Series ) چیست؟

سری مک‌لورن همان سری تیلور حول نقطه $ x=0 $ است. بنابراین تعریف زیر را برای آن خواهیم داشت:

تعریف سری مک‌لورن:

فرض کنید $ f(x) $ یک تابع حقیقی است که در نقطه $ x = 0 $‌ بی‌نهایت بار مشتق پذیر می‌باشد. سری مک‌لورن تابع $ f(x) $  را در نقطه‌ی $ x = 0 $ به صورت زیر ارائه می‌دهد:

$ \sum_{n=0}^{\infty} f^{(n)} (0) \frac{x^{n}}{n!} = f(0) + f^{\prime} (0) x + f^{\prime\prime} (0) \frac{x^{2}}{2!} + f^{(3)} (0) \frac{x^{3}}{3!} + \cdots + f^{(3)} (0) \frac{x^{3}}{3!} + \cdots $

که به آن سری مک‌لورن تابع $ f(x) $‌ می‌گوییم.

توجه داشته باشید که در فرمول بالا، $ f^{(n)} (0) $ به معنی مشتق  $ n $‌م تابع $ f(x) $  در نقطه‌ی $ x = 0 $ است.

به سری مک‌لورن، بسط مک‌لورن نیز گفته می‌شود.

روش محاسبه سری مک‌لورن:

برای محاسبه سری مک‌لورن یک تابع، ابتدا مقدار تابع را در نقطه $ x=0 $ به دست می‌آوریم. سپس مشتق تابع را گرفته و مقدار مشتق را در نقطه $ x=0 $ محاسبه می‌کنیم. پس از آن به ترتیب مشتق مرتبه دوم و سوم و ... را در نقطه $ x=0 $ محاسبه می کنیم. سپس مقادیر به دست آمده را در فرمول بالا جایگذاری کرده و بسط مک‌لورن تابع به دست خواهد آمد.

اکنون با یک مثال به خوبی روش کار را ببینیم.

مثال: بسط مک‌لورن تابع $ \cos x $ را به دست آورید.

حل: در این مثال $ f(x) = \cos x $. ابتدا مقدار تابع در این نقطه را محاسبه می کنیم و سپس مشتقات تابع را در این نقطه حساب می‌کنیم.

$ f(x) = \cos x \Longrightarrow f (0) = \cos (0) = 1 $

$ f(x) = \cos x \Longrightarrow f^{\prime} (x) = - \sin (x)  \Longrightarrow f^{\prime} (0) = - \sin (0) = 0 $

$ f^{\prime}(x) = - \sin (x) \Longrightarrow f^{\prime\prime} (x) = - \cos (x)  \Longrightarrow f^{\prime\prime} (0) = - \cos (0) = -1 $

$ f^{\prime\prime}(x) = - \cos (x) \Longrightarrow f^{(3)} (x) =  \sin (x)  \Longrightarrow f^{(3)} (0) =  \sin (0) = 0 $

$ f^{(3)}(x) = \sin (x) \Longrightarrow f^{(4)} (x) =  \cos (x)  \Longrightarrow f^{(4)} (0) =  \cos (0) = 1 $

و به همین ترتیب مشتق مراتب بالاتر در نقطه $ x = 0 $  به صورت زیر تکرار خواهد شد:

$  f^{(5)} (0) = 0  , f^{(6)} (0) = -1  , f^{(7)} (0) = 0  , f^{(8)} (0) = 1  , f^{(9)} (0) = 0  , \cdots  $

بنابراین سری مک‌لورن تابع $ \cos x $ با جایگذاری مقادیر فوق در فرمول، به صورت زیر خواهد بود:

$ \begin{align*}  \sum_{n=0}^{\infty} f^{(n)} (0) \frac{x^{n}}{n!} &= f(0) + f^{\prime} (0) x + f^{\prime\prime} (0) \frac{x^{2}}{2!}  + f^{(3)} (0) \frac{x^{3}}{3!} + \cdots \\  &= 1 +  0 \times x - 1 \times \frac{x^{2}}{2!}  + 0 \times \frac{x^{3}}{3!} + 1 \times \frac{x^{4}}{4!} + 0 \times \frac{x^{5}}{5!} \\ & \qquad - 1 \times \frac{x^{6}}{6!} + 0 \times \frac{x^{7}}{7!} + 1 \times \frac{x^{8}}{8!} + 0 \times \frac{x^{9}}{9!} - \cdots  \\ & = 1 -\frac{x^{2}}{2!} +  \frac{x^{4}}{4!} - \frac{x^{6}}{6!} +\frac{x^{8}}{8!} - \cdots  \end{align*} $

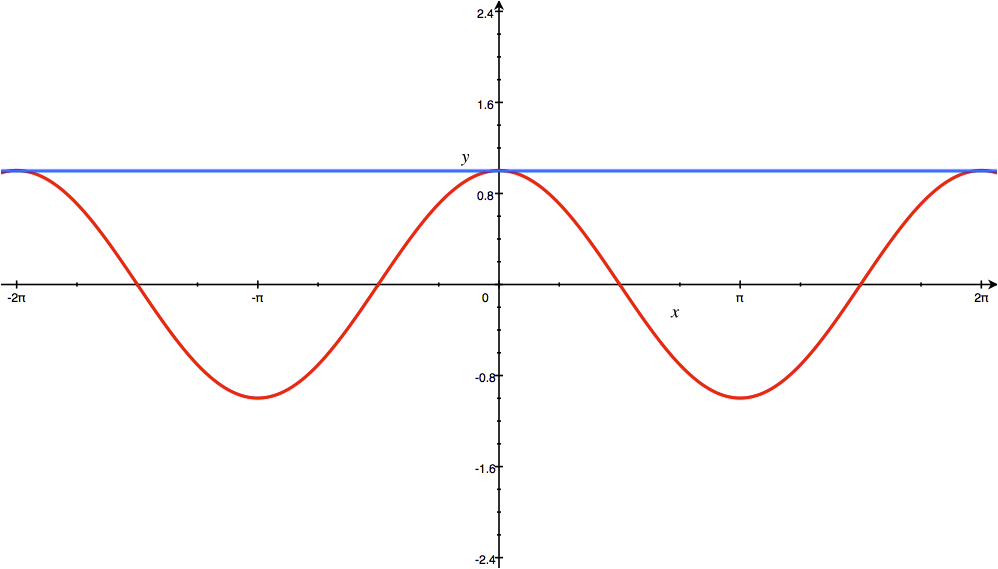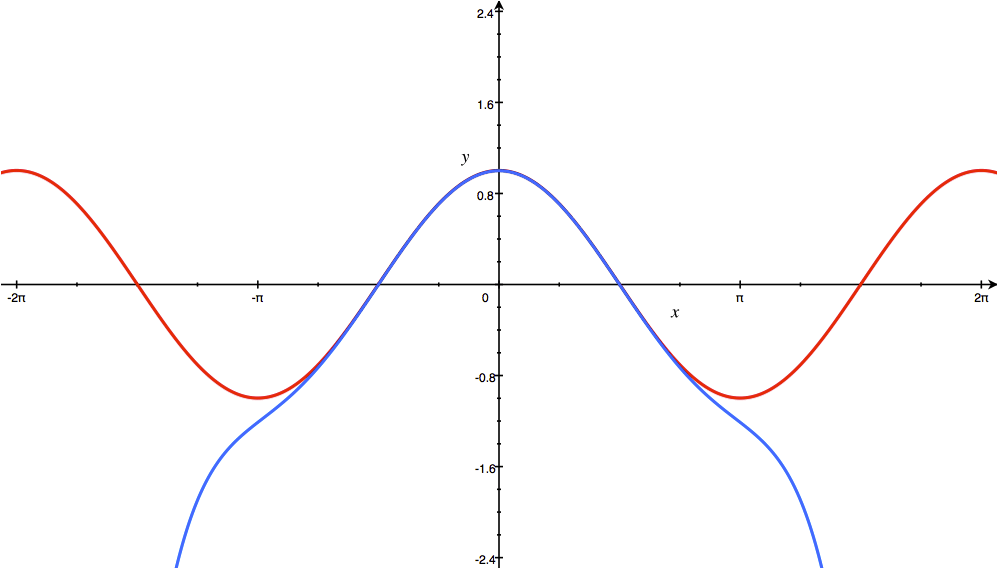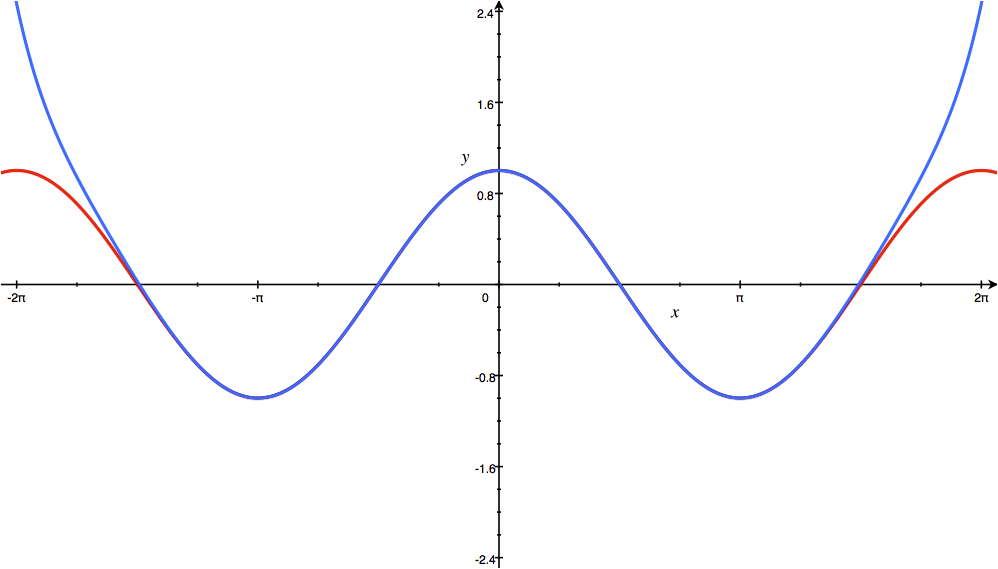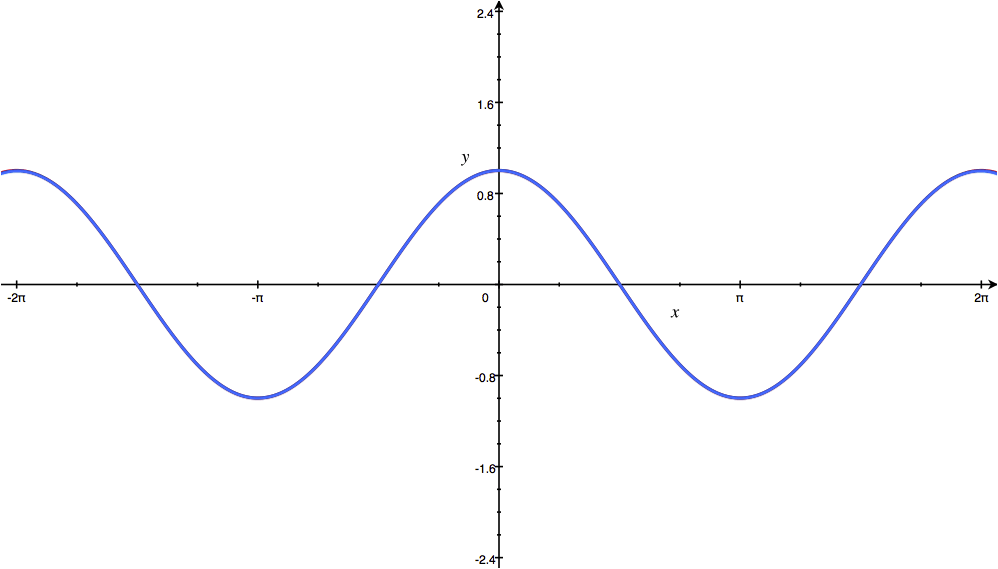
این چندجمله‌ای سری مک‌لورن تابع $ \cos x $ می‌باشد. هرچه تعداد مراتب مشتق را بیشتر کنیم، دقت تخمین سری بیشتر خواهد شد و منحنی چندجمله‌ای بر منحنی تابع منطبق‌تر خواهد شد. نمودار این چندجمله‌ای را به ازای درجه‌های مختلف در زیر مشاهده می‌کنید.

تمرین ۱: سری مک‌لورن تابع $ f(x) = \tan x $ بیابید.

تمرین ۲: سری مک‌لورن تابع $ f(x) = \cot x $ بیابید.

در مطالب بعدی، سری مک‌لورن تعدادی از توابع خاص را با هم محاسبه خواهیم کرد. با ما همراه باشید.