آزمون میان ترم جبر 2 دکتر مشایخی 15/10/1384 فردوسی مشهد

نام آزمون : میان ترم جبر 2

نام استاد : دکتر مشایخی

تاریخ برگزاری : 15/10/1384

دانشگاه : فردوسی مشهد

دانشکده : علوم ریاضی

۱. می دانیم مرکز هر p-گروه متناهی غیر بدیهی است. اکنون فرض کنید G یک گروه از مرتبه ی p3 باشد ( p عدد اول است). ثابت کنید گروه آبلی است . سپس مرتبه 'G را بدست آورید.

۲. فرض کنید 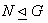و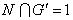 . ثابت کنید 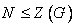و .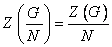

۳. اگر G گروه پوچ توانی باشد و 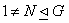آنگاه ثابت کنید .

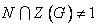۴. فرض کنید F یک میدان باشد. ثابت کنید هر ایده آل اول غیر صفر 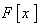یک ایده آل پیشین است.

۵. ثابت کنید در میدان F با مشخصه ی p ( عدد اول ) برای هر عضو a از F چند جمله ای 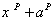تحویل پذیر است.

۶. فرض کنیم E یک توسیع متناهی از F از درجه ی عدد اول p باشد. ثابت کنید E یک توسیع ساده از F است.

۷. ثابت کنید .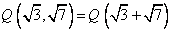

۸. ثابت کنید هر توسیع متناهی از 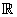یا خود 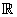است و یا .

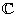۹. فرض کنیم E یک توسیع میدان از F است و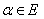 روی F متعالی باشد. ثابت کنید هر عضو 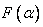که در F نیست روی F متعالی است.