آزمون جبر 2 قسمت گروه ها دکتر مشایخی 2/9/1384 فردوسی مشهد
نام آزمون: جبر 2 قسمت گروه ها
نام استاد : دکتر مشایخی
تاریخ برگزاری : 2/9/1384
دانشگاه : فردوسی مشهد
دانشکده : علوم ریاضی
۱. فرض کنید G یک گروه پوچ توان و K زیرگروهی از آن باشد.
الف : ثابت کنید زیرگروه هایی از G مانند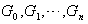 موجودند بطوری که
موجودند بطوری که 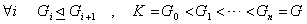 .
.
ب : ثابت کنید اگر 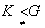 آنگاه
آنگاه 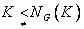 .
.
۲. الف : ثابت کنید یک گروه آبلی نامتناهی نمی تواند یک سری ترکیبی داشته باشد.
ب : فرض کنید G گروهی حل پذیر باشد. ثابت کنید G متناهی است اگر و فقط اگر G دارای یک سری ترکیبی باشد.
۳. اولا ً سری مشتق گروه G را تعریف کنید . ثانیا ً نشان دهید در گروه های حل پذیر طول سری مشتق از طول هر سری آبلی کوچکتر یا مساوی است.
۴. فرض کنید 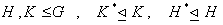 . ثابت کنید
. ثابت کنید 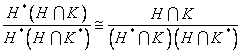 .
.
نمونه سوال امتحانی, 1384, دانشگاه فردوسی مشهد, نمونه سوالات دانشگاهی, نمونه سوالات جبر2, نمونه سوالات دکتر مشایخی
- بازدید: 16796