Geometry of Manifolds-Final MSc. Exam-1386-10-15
Geometry of Manifolds
Final MSc. Exam
Department ofMathematics Ferdowsi University ofMashhad
1386-10-15
Dr H.ghane
1. Let M be a 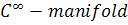
and 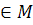 . if
. if 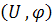
is a chart at P with coordinate function 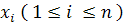
, then show that 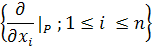
Is a basis for 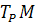 .
.
2.
Let 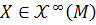
. Show that for each 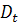
is an open set in M and 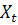
is a diffeomorphism of 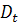
onto 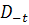
with inverse 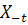 .
.
3.
Let M be a connected Riemannian manifold and 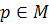
. let 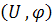
be a chart at P with 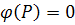 and
and 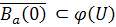
. suppose 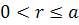 and
and 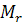 and
and 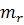
denote the maximum and minimum value of mapping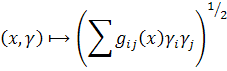
. if we have the following inequality
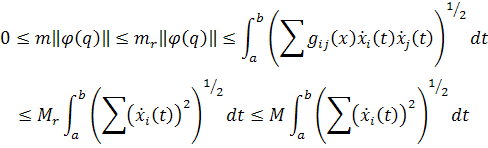
Show that M is a metric space with metric 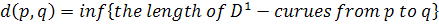 and
and
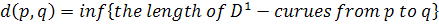 and
and
its manifold topology and metric topology are equalent.
4.
4.
Show that if 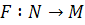 is
is 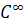 and
and 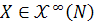
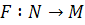 is
is 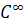 and
and 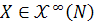
then an F-related vector field Y on M , if it exists, is uniquely determined iff 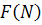
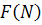
is dense in M.
5.
5.
Show that 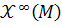
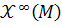
is infinite dimensional over 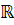
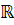
but locally finitely generated over 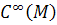
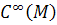
, i.e. each 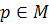
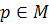
has a neighborhoodV on which there is a finite set of vector fields wich generated 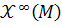 as a
as a 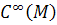
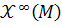 as a
as a 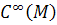
module.
6.
6.
Show that iffis a 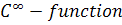
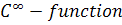
a closed regular submfd N of M then f is restriction of a 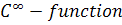
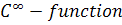
on M.
نمونه سوال امتحانی, نمونه سوالات دانشگاهی, نمونه سوالات کارشناسی ارشد
- بازدید: 31967