1386/9/26 Midterm Geometry of manifolds Dr. H.Ghane
Geometry of manifolds
Midterm MSc. Exam
Department of MathematicsFerdowsiUniversity of Mashhad
1386/9/26
Dr. H.Ghane’
1. Let 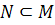 be a regular submanifold of M. show that
be a regular submanifold of M. show that 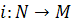 ( inclusion map ) is an imbedding.
( inclusion map ) is an imbedding.
2. If H is a regular submanifold and subgroup of a Lie group G , then H is closed as asubset of G.
3. Show that real projective space 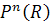 is a
is a 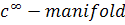 .
.
4. Let M and N be two 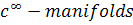 with dimension m and n respectively with
with dimension m and n respectively with 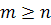 . let
. let 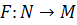 be a 1-1 immersion . show that F is an open mapping .
be a 1-1 immersion . show that F is an open mapping .
5. Show that 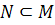 is an n-dimentional submanifold of
is an n-dimentional submanifold of 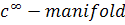 M with dimension n if and only if it is an open submanifold ofM.
M with dimension n if and only if it is an open submanifold ofM.
6. Let G be a Lie grup and 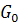 denote the connected component of G containing the identity element e. show that
denote the connected component of G containing the identity element e. show that 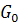 is the only connected open subgroup of G.
is the only connected open subgroup of G.
7. Show that 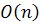 acts transitively on
acts transitively on 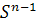 and determine the isotropy subgroup of
and determine the isotropy subgroup of 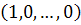 .
.
- بازدید: 27207