Written by مدیریت سایت ریاضیات ایران on 04 مرداد 1386. Posted in نمونه سوالات مباني رياضيات.

مباني رياضيات دکتر حجازیان دیماه 1383

به نام خدا

اللهم صل علي محمد و آل محمد

1. ثابت كنيد اگر مجموعه ي A به قسمي باشد كه هر ابر مجموعه ي سره ي A نامتناهي باشد ، آنگاه A نامتناهي است.

2. فرض كنيد C قطعه اي از منحني 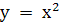باشد كه 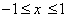. ثابت كنيد C ناشمارا است.

3. اگر A مجموعه اي باشد از بازه هاي جدا از هم در 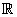، ثابت كنيد A شماراست ( توجه كنيد كه اعضاي A بازه هاي جدا از هم هستند. )

4. فرض كنيد X يك مجموعه باشد ، ثابت كنيد .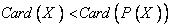

5. اگر a و b اعداد اصلي باشند، ثابت كنيد مجموعه هاي مجزاي A و B وجود دارند كه 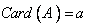و .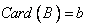

6. اگر A يك مجموعه 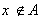و و 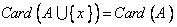. ثابت كنيد A نامتناهي است.

7. فرض كنيد 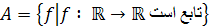. رابطه ي 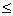روي A را به صورت زير تعريف مي كنيم:

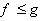اگر به ازاي هر .

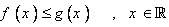آ: ثابت كنيد 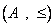يك مجموعه ي مرتب جزئي است.

ب: يك زنجير در A مثال بزنيد.

پ: اگر 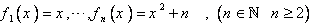و 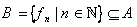بررسي كنيد در B كداميك از عناصر زير موجود است ؟ در صورت وجود آن را معرفي كنيد.

الف: عنصر ماكسيمال

ب: عنصر مينيمال

پ: عنصر ماكزيمم

ت: عنصر مينيمم.

8. اگر P افرازي از مجموعه ي ناتهي X باشد ، ثابت كنيد مجموعه ي 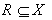موجود است كه به ازاي هر 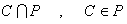از يك و فقط يك عضو تشكيل شده است.