ميان ترم آناليز رياضي1،فردوسی مشهد،حجازيان ترم اول 85-84

به نام خدا

اللهم صل علی محمد و آل محمد

نام آزمون: ميان ترم آناليز رياضي 1

نام استاد: دکتر حجازيان

تاريخ برگزاري: ترم اول سال تحصيلی 85-1384

دانشگاه: فردوسي مشهد

دانشکده: علوم رياضي

1. يک مجموعه فشرده در يک فضاي متري را تعريف کنيد. فرض کنيد 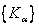گردايه اي از زيرمجموعه هاي فشرده ي ناتهي فضاي متري X باشد که اشتراک هر تعداد متناهي از اعضاي آن ناتهي است. ثابت کنيد .
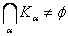2. نقطه ي حدي يک زيرمجموعه E از فضاي متري X را تعريف کنيد. اگر 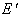مجموعه ي نقاط حدي E باشد، ثابت کنيد 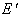بسته است.
3. اگر 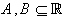، ثابت کنيد .
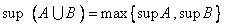4. براي مجموعه ي 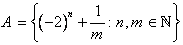، 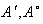را با ذکر دليل بيابيد. سپس 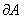را بدست آوريد.
5. يک مجموعه ي همبند را تعريف کنيد. نشان دهيد اگر 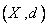همبند باشند ولي کراندار نباشند آنگاه به ازاي 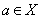هر و هر 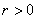، 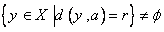. با مثال هايي نشان دهيد که مفروضات همبندي و کراندار نبودن X ضروري مي باشد.
6. ثابت کنيد فضاي متري X همبند است اگر و فقط اگر هر زير مجموعه ي ناتهي و سره ي X داراي مرز ناتهي باشد.
7. ثابت کنيد 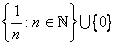در 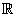فشرده است.