میان ترم آنالیز ریاضی1، فردوسی مشهد، ابراهیمی ویشکی 13840821

به نام خدا

اللهم صل علی محمد و آل محمد

نام آزمون: ميان ترم آناليز رياضي 1

نام استاد: دکتر ابراهيمي ويشکي

تاريخ برگزاري: 13840821

دانشگاه: فردوسي مشهد

دانشکده: علوم رياضي و آمار

1. نامساوي هاي هولدر و مينکونسکي را در 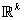بيان کنيد و يکي را به دلخواه اثبات کنيد.

2. i – مجموعه ي باز را در يک فضاي متريک تعريف کنيد.

ii - نشان دهيد شرط لازم و کافي براي آنکه G در فضاي متريک X باز باشد آن است که براي هر مجموعه ي A در X ، .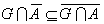

iii – نشان دهيد که اگر G و A در X چگال باشند و G باز باشد آنگاه 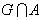نيز چگال است. با مثالي نشان دهيد که شرط باز بودن G اساسي است.

3. مجموعه ي کراندار را در يک فضاي متريک تعريف کنيد. سپس نشان دهيد که شرط لازم و کافي براي آنکه مجموعه ي A در فضاي متريک 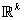کراندار باشد آن است که M>0 موجود باشد به طوري که براي هر .

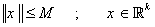4. دنباله ي کشي را در يک فضاي متريک تعريف کنيد. نشان دهيد شرط لازم و کافي براي آنکه يک دنباله ي کشي همگرا باشد آن است که لااقل يک زيردنباله ي همگرا داشته باشد.

5. نشان دهيد که بازه ي 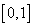در فضاي 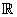فشرده است اما بازه ي 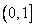فشرده نيست.