تشخیص معادله دیفرانسیل کامل
به نام خدا
الـهم صل علی مـحمد و آل محـمد
در اين درس ابتدا در قضيه ي 1، يک شرط لازم و کافي براي تشخيص کامل بودن ِ يک معادله ديفرانسيل را بيان کرده و اثبات مي کنيم و سپس در مثالي، چگونگي استفاده از اين قضيه را نشان مي دهيم :
قضيه 1.2: فرض کنيد در معادله ي
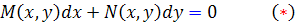
توابع M و N توابعي پيوسته باشند. در اين صورت اين معادله کامل است اگر و تنها اگر
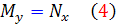
که در آن 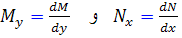 .
.
اثبات: ابتدا فرض کنيم معادله ي  کامل باشد، پس تابعي مانند f وجود دارد به طوري که شرايط برقرارند. از حساب ديفرانسيل و انتگرال به ياد داريم که چون M و N پيوسته اند، مشتقات جزئي مرتبه دوم زير با هم برابرند :
کامل باشد، پس تابعي مانند f وجود دارد به طوري که شرايط برقرارند. از حساب ديفرانسيل و انتگرال به ياد داريم که چون M و N پيوسته اند، مشتقات جزئي مرتبه دوم زير با هم برابرند :
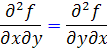
بنابراين
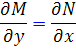
يا به عبارت ساده تر 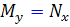 . پس اگر معادله
. پس اگر معادله  کامل باشد، تساوي
کامل باشد، تساوي 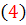 برقرار است.
برقرار است.
اکنون فرض کنيم تساوي 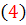 برقرار باشد، نشان مي دهيم معادله ي
برقرار باشد، نشان مي دهيم معادله ي  کامل است. يعني بايد تابع ثابت f را بيابيم. اين تابع بايد در تساوي هاي
کامل است. يعني بايد تابع ثابت f را بيابيم. اين تابع بايد در تساوي هاي 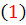 صدق کند. از نخستين ِ تساوي ِ آن داريم :
صدق کند. از نخستين ِ تساوي ِ آن داريم :
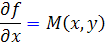
با اتگرال گيري نسبت به x ، تابع f محاسبه مي شود :
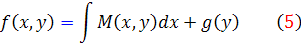
که 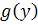 ، ثابت انتگرال گيري ، تابعي از y است. اکنون تساوي دوم از تساوي هاي
، ثابت انتگرال گيري ، تابعي از y است. اکنون تساوي دوم از تساوي هاي  را بررسي مي کنيم . پس :
را بررسي مي کنيم . پس :
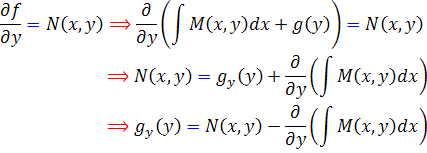
سپس با انتگرال گيري از 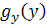 نسبت به y ، تابع g به صورت زير خواهد بود:
نسبت به y ، تابع g به صورت زير خواهد بود:
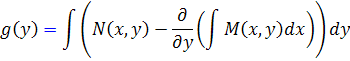
که تابع زير انتگرال، بايد تابعي از y باشد، يعني بايد مشتق آن نسبت به x صفر شود. پس :
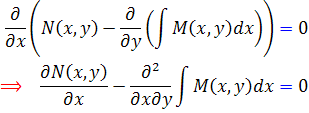
اما 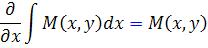 پس بايد داشته باشيم:
پس بايد داشته باشيم:
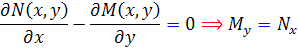
اما اين رابطه، فرض ما بود و از ابتدا درست فرض کرديم. پس تابع f که در رابطه ي 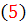 بيان شد، جواب عمومي معادله است.
بيان شد، جواب عمومي معادله است.
ضمن اثبات قضيه ي 1 ، يک روش براي حل معادله ديفرانسيل کامل بيان شد کهبه طور خلاصه اين گونه است:
اگر معادله ي  کامل باشد، از
کامل باشد، از 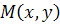 نسبت به x انتگرال مي گيريم و ثابت انتگرال گيري را تابعي بر حسب y مانند
نسبت به x انتگرال مي گيريم و ثابت انتگرال گيري را تابعي بر حسب y مانند 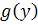 در نظر مي گيريم. سپس از معادله ي به دست آمده، بر حسب y مشتق مي گيريم و آن را مساوي با
در نظر مي گيريم. سپس از معادله ي به دست آمده، بر حسب y مشتق مي گيريم و آن را مساوي با 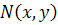 قرار مي دهيم تا تابع
قرار مي دهيم تا تابع 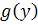 به دست آيد.
به دست آيد.
همچنين مي توانيم از تابع 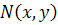 نسبت به y انتگرال بگيريم وثابت انتگرال گيري را تابعي بر حسب x مانند
نسبت به y انتگرال بگيريم وثابت انتگرال گيري را تابعي بر حسب x مانند 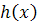 در نظر بگيريم. سپس از معادله ي به دست آمده، برحسب x مشتق بگيريم و آن را مساوي با
در نظر بگيريم. سپس از معادله ي به دست آمده، برحسب x مشتق بگيريم و آن را مساوي با 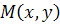 قرار دهيم تا
قرار دهيم تا 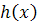 به دست آيد.
به دست آيد.
مثال 12.2: ابتدا نشان دهيد معادله ديفرانسيل 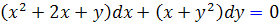 کامل است سپس جواب عمومي آن را محاسبه کنيد .
کامل است سپس جواب عمومي آن را محاسبه کنيد .
حل: در اين مثال 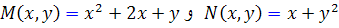 و
و 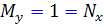 . پس معادله ي داده شده کامل است. براي به دست آوردن جواب عمومي از روشي که در اثبات قضيه ي 1 معرفي شد، استفادهمي کنيم :
. پس معادله ي داده شده کامل است. براي به دست آوردن جواب عمومي از روشي که در اثبات قضيه ي 1 معرفي شد، استفادهمي کنيم :
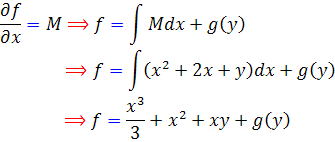
و 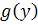 را به ترتيب زير به دست مي آوريم . مي دانيم
را به ترتيب زير به دست مي آوريم . مي دانيم 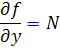 بنابراين با قرار دادن مقادير N و
بنابراين با قرار دادن مقادير N و 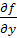 داريم :
داريم :
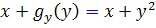
پس
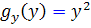
. بنابراين
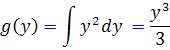
پس تابع f به صورت زير خواهد بود :
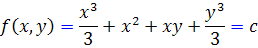
که اين جواب عمومي معادله ي داده شده است.
[/tab_item] [/tabs]- بازدید: 29522