روش دوم محاسبه جواب عمومی معادله کامل
به نام خدا
الـهم صل علی مـحمد و آل محـمد
در قضيه 2 روش ديگري براي به دست آوردن تابع f ( جواب معادلات ديفرانسيل کامل )ارائه مي دهيم و در مثال 13 با استفده از اين قضيه، به حل يک معادله ديفرانسيل کامل مي پردازيم :
قضيه 2.2: اگر معادله ي
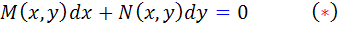
در بازه ي R کامل باشد، آنگاه جواب عمومي آن به صورت زير است:
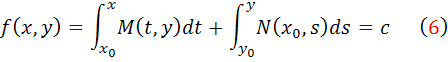
که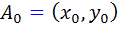 
نقطه اي از R است به طوري که براي هر 
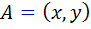از R ، خط شکسته ي 
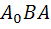که 
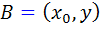، در R باشد. شکل زير را ببينيد :
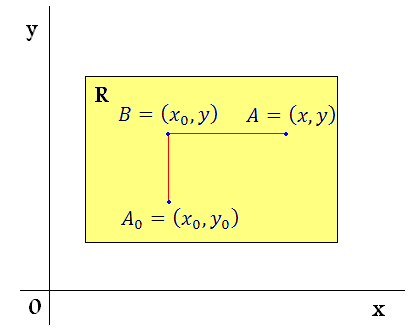
اثبات: اگر قرار باشد تابع داده شده ي f ، جواب معادله ديفرانسيل 
باشد، بايستي در تساوي هاي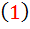 
صدق کند . درستي اين مطلب را تحقيق مي کنيم:
چون
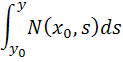
مستقل از x است پس :
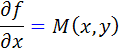
اما
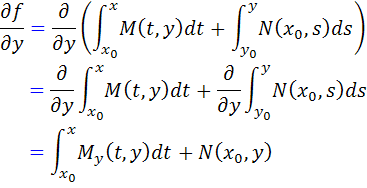
اما مي دانيم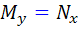 
، پس :
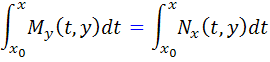
و بنابراين
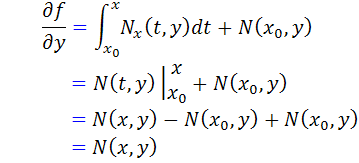
بنابراين تابع f ، معرفي شده در 
جواب عمومي معادله کامل است.
مثال 13.2: جواب عمومي معادله ديفرانسيل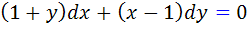 
را بيابيد .
حل: در اين مثال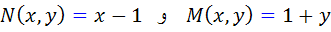 
. پس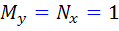 
و معادله کامل است.
مستطيل R را تمام صفحه در نظر مي گيريم و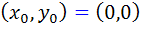 
. بنابراين براي هر 
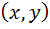جواب عمومي به صورت زير است :
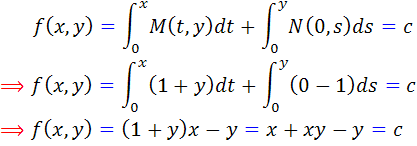
که مي توان آن را به صور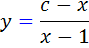ت 
نوشت.
- بازدید: 17709