مزدوج ماتریس
مزدوج ماتریس: فرض کنید که $A$ یک ماتریس از مرتبه $ m \times n$ باشد. ماتریسی که از مزدوج کردن تک تک درایههای ماتریس $A$ حاصل میشود، را مزدوج ماتریس $A$ گویند. به عبارت دیگر فرض کنید $A = [a_{ij}]$ باشد. در اینصورت مزدوج ماتریس $A$ را با نماد $\overline{A} = [b_{ij}]_{m \times n}$ نمایش میدهند، که رابطه زیر بین درایههای $A$ و $\overline{A}$ برقرار میباشد:
$b_{ij} = \overline{a_{ij}}$
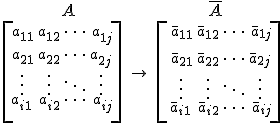
مثال ۱. مزدوج ماتریسهای زیر را محاسبه کنید.
۱. $A = \begin{bmatrix} 1 & 5i & i \\ 2 & 0 & i+1 \end{bmatrix} \Longrightarrow \overline{A} = \begin{bmatrix} 1 & -5i & -i \\ 2 & 0 & 1-i \end{bmatrix}$
۲. $B = \begin{bmatrix} 5i+3 & 2i+1 \\ 3i+7 & 5i \end{bmatrix} \Longrightarrow \overline{B} = \begin{bmatrix} 3-5i & 1-2i \\ 7-3i & -5i \end{bmatrix}$
تمرین ۱. مزدوج ماتریسهای زیر را بدست آورید.
۱. $A = \begin{bmatrix} 1 & i & 2i+1 \\ \frac{5i+1}{2i} & 0 & \frac{2i+1}{3i} \end{bmatrix}$
۲. $B = \begin{bmatrix} 1+ \sqrt{2i} & 5 \\ 0 & (3i+5)(2i+1) \end{bmatrix}$
- بازدید: 14580