ماتریس متقارن

تعریف ماتریس متقارن: فرض کنید که A یک ماتریس مربعی از مرتبه $ n $ باشد. ماتریس A را متقارن گویند، هرگاه با ترانهاده اش برابر باشد یعنی داشته باشیم:

$ A^{T} = T $

در واقع این عبارت بالا بیان می‌کند که در ماتریس متقارن A رابطه زیر بین داریه‌های ماتریس برقرار باشد.

$ \forall 1 \leq i , j \leq n     ⇒      a_{ij} = a_{ji} $

به زبان ساده تر این که وقتی یک ماتریس متقارن است، درایه‌های آن نسبت به قطر اصلی متقارن می‌باشند و برعکس اگر درایه های ماتریسی نسبت به قطر اصلی متقارن باشند آن ماتریس را ماتریس متقارن گوییم.

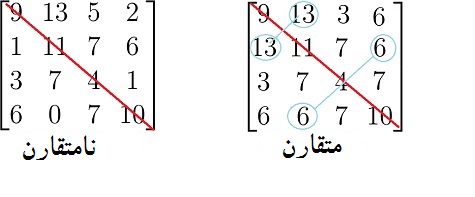
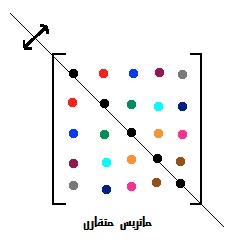
مثال ۱. کدام یک از ماتریسهای زیر متقارن هستند.

۱. $ A = \begin{bmatrix} 1 & 2 & 3 \\ 2 & 0 & 1 \\ 3 & 1 & 5 \end{bmatrix} $

ماتریس A متقارن است، زیرا در آن درایه‌ها نسبت به قطر اصلی متقارن می‌باشند.

۲. $ B = \begin{bmatrix} 5 & 3 & 0 \\ i & 0 & 1 \\ 0 & 1 & 0 \end{bmatrix} $

ماتریس B متقارن نیست، زیرا در آن درایه‌ها نسبت به قطر اصلی متقارن نمی‌باشند.

مثال ۲. به ازای چه مقادیری از x و y ماتریس زیر متقارن است؟

$ A = \begin{bmatrix} 5 & 2 & 1 \\ x+y & 0 & 1 \\ y-x & 1 & 5 \end{bmatrix} $

چون ماتریس A متقارن می‌باشد، در اینصورت درایه‌های این ماتریس باید نسبت به قطر اصلی متقارن باشند. پس با توجه به این موضوع که $ x+y = 2 , y-x =1$ لذا داریم:

⇒ $ x+y = 2 \rightarrow x = 2 - y $

⇒ $ y = x+1 \rightarrow y = 2-y+1 \rightarrow 2y = 3 \rightarrow y = \frac{3}{2} \rightarrow x = - \frac{1}{2} $

تمرین ۱. به ازای چه مقادری از $ x,y,z $  ماتریسهای زیر متقارن خواهند بود؟

۱. $ A = \begin{bmatrix} 1 & 5 & x+y \\ z & 2 & y \\ 1 & x & 0 \end{bmatrix} $

۲. $ B= \begin{bmatrix} 0 & 5 & 0 \\ x+y & 1 & 2 \\ 0 & 2x+y & 3 \end{bmatrix} $

۳. $ C = \begin{bmatrix} 5 & 2x+z & y \\ 1 & 0 & 1 \\ i & 2z & 0 \end{bmatrix} $