میان ترم ریاضی عمومی 3 دکترصابری نجفی 27/2/1385 فردوسی مشهد

به نام خدا

اللهم صل علی محمد و آل محمد

نام آزمون: ميان ترم رياضي عمومي 3

تاريخ برگزاري: 27/2/1385

نام استاد: دکتر صابري نجفي

دانشگاه: فردوسي مشهد

دانشکده: علوم رياضي

رشته: رياضي

1. اولا ً: ثابت کنيد 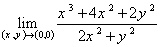برابر با 2 است.

ثانيا ً: نشان دهيد حد زير موجود نيست :

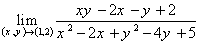
2. اولا ً: اگر f يک تابع از دو متغير x و y باشد به طوري که 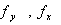در يک ناحيه ي باز R پيوسته باشد، آنگاه f در R ديفرانسيل پذير است.

ثانيا ً: به کمک مفهوم ديفرانسيل يک تابع سه متغيره که خود تعريف مي کنيد، مقدار تقريبي عبارت زير را حساب کنيد.

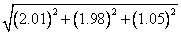
3. اگر 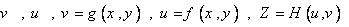معادلات زير را که موسوم به معادلات کوشي-ريمان هستند صدق کنند:

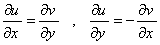
نشان دهيد:

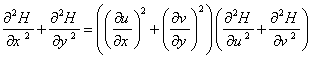
4. مقدار مشتق سوئي تابع 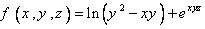را در نقطه ي 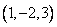و در امتداد بردار 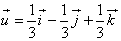حساب کنيد.

5. فرمول تيلور را در 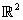ثابت کرده و با استفاده از آن تابع 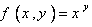را در مجاورت نقطه ي تا جمله ي درحه دوم بسط دهيد.

6. اولا ً: نقاط بحراني تابع 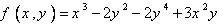را بدست آوريد و سپس انواع آن را تعيين کنيد.

ثانيا ً: صفحه ي x+y+z=12 سهمي وار به معادله ي 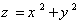را در يک بيضي تلاقي مي کند. نقطه اي بر روي اين بيضي بيابيد که نزديکترين فاصله تا مبداء مختصات را داشته باشد.