خانه

اعمال جبری اعداد مختلط: در این مطلب سعی داریم اعمال جبری که بر روی اعداد مختلط تعریف می‌شوند، را بیان کنیم.

جمع اعداد مختلط:

فرض کنید که دو عدد مختلط $z_1 = a + ib $ و $ z_2 = c + id $ موجود باشند. در اینصورت عمل جمع بر روی اعداد مختلط به گونه زیر تعریف می‌شود:

$ z_1 + z_2 = (a + ib) + (c +id) = (a+c) + (c+d)i $

در واقع در عمل جمع اعداد مختلط، کافی است که قسمت‌های حقیقی را با هم و قسمت‌های موهومی را نیز با هم جمع کنیم.

مثال ۱. جمع اعداد مختلط زیر را بدست آورید.

۱. $  (2i+5) + 5i + i = 8i + 5 $

۲. $ (16i +1) - 12i+3 = 4i+4 $

۳. $  4+4i - (4-4i) = 8i $

۴. $  (2i+1) + (5+3i) +2i = 7i + 6 $

ضرب دو عدد مختلط:

فرض کنید که دو عدد مختلط $z_1 = a + ib $ و $ z_2 = c + id $ موجود باشند. در اینصورت عمل ضرب بر روی اعداد مختلط به گونه زیر تعریف می‌شود:

$ z_1 . z_2 = (a + ib) (c +id) = (ac - bd) +i (bc + ad) $

مثال ۲. عبارات زیر را محاسبه کنید.

۱. $ 2i (2i+1) + 5i (7i+2) = -4 + 2i + 10i - 35 = 12i -39 $

۲. $ (12i+5) (2i+7) - (6i(2i(2i+1))) = (35 - 24) + (84 + 10)i - (6i(-4+2i)) = 11 + 94i + 24i + 12i = 33 + 118i $

تمرین ۱. عبارات زیر را محاسبه کنید.

۱. $(2i)i (i+5)(2i+1) +3i =$

۲. $2i ((2i+1) . (5i+3)) + 15i =$

۳. $(15i+1)(1+2) - (5i+3)(7i+1) =$

۴. $(6i+2) (i-1) + 5= $

تقسیم اعداد مختلط:

فرض کنید که دو عدد مختلط $z_1 = a + ib $ و $ z_2 = c + id $ موجود باشند. در اینصورت برای عمل تقسیم بر روی اعداد مختلط به گونه زیر عمل می‌شود:

 فرض کنید حاصل تقسیم $ \frac {z_1}{z_2} = \frac {a+ib}{c+id} $ را از شما می‌خواهند. برای محاسبه این تقسیم باید صورت و مخرج را در مزدوج عدد مخرج ضرب کنیم، در نتیجه خواهیم داشت:

$ \frac {z_1}{z_2} = \frac {a+ib}{c+id} = \frac{(a+ib)(c-id)}{(c+id)(c-id)} = \frac {(ac+bd) + i(bc-ad)}{c^2 + d^2} = \frac {ac+bd}{c^2 + d^2}+i \frac {bc-ad}{d^2+c^2}$

مثال ۳. تقسیم‌های زیر را محاسبه کنید.

۱. $  \frac{2i+5}{3i+7} = \frac {(2i+5)(3i+7)}{9+49} = \frac {(35+6)+(-15+14)i}{58} = \frac {41-i}{58} \rightarrow \frac {41}{58} - \frac {1}{58}i $

۲. $ \frac {12i(5i+3)}{2i} = \frac {-60+36i}{2i} = \frac {(-60+36i)(-2i)}{(2i)(-2i)} = \frac {(120i + 72)}{4} = \frac {120i}{4} + \frac{72}{4} $

تمرین ۲. عبارات زیر را محاسبه کنید.

۱. $ \frac {2i(5i+3)7i}{(5i+9)(6i+1)} $

۲. $  \frac {7i(9i)-6}{(5i+3)^2} $

۳. $ \frac {(16i+1)(-16+1)}{(2i+3)^2} $

مزدوج یک عدد مختلط: فرض کنید که $p= a + ib $ یک عدد مختلط باشد. مزدوج مختلط این عدد را به گونه زیر تعریف می‌کنیم:

$ \overline{p} = a - ib $

که عبارت فوق، از تغییر علامت قسمت موهومی عدد مختلط $p$ به دست می‌آید. مزدوج مختلط عدد $p$ را با نماد $ \overline{p}$ نمایش می‌دهند. 

برای نمایش هندسی یک عدد مختلط، دستگاه مختصات زیر را در نظر بگیرید. در واقع در صفحه مختلط، مزدوج عدد مختلط p، قرینه نقطه متناظر با آن عدد بر روی صفحه مختلط، نسبت به محور xها می‌باشد.

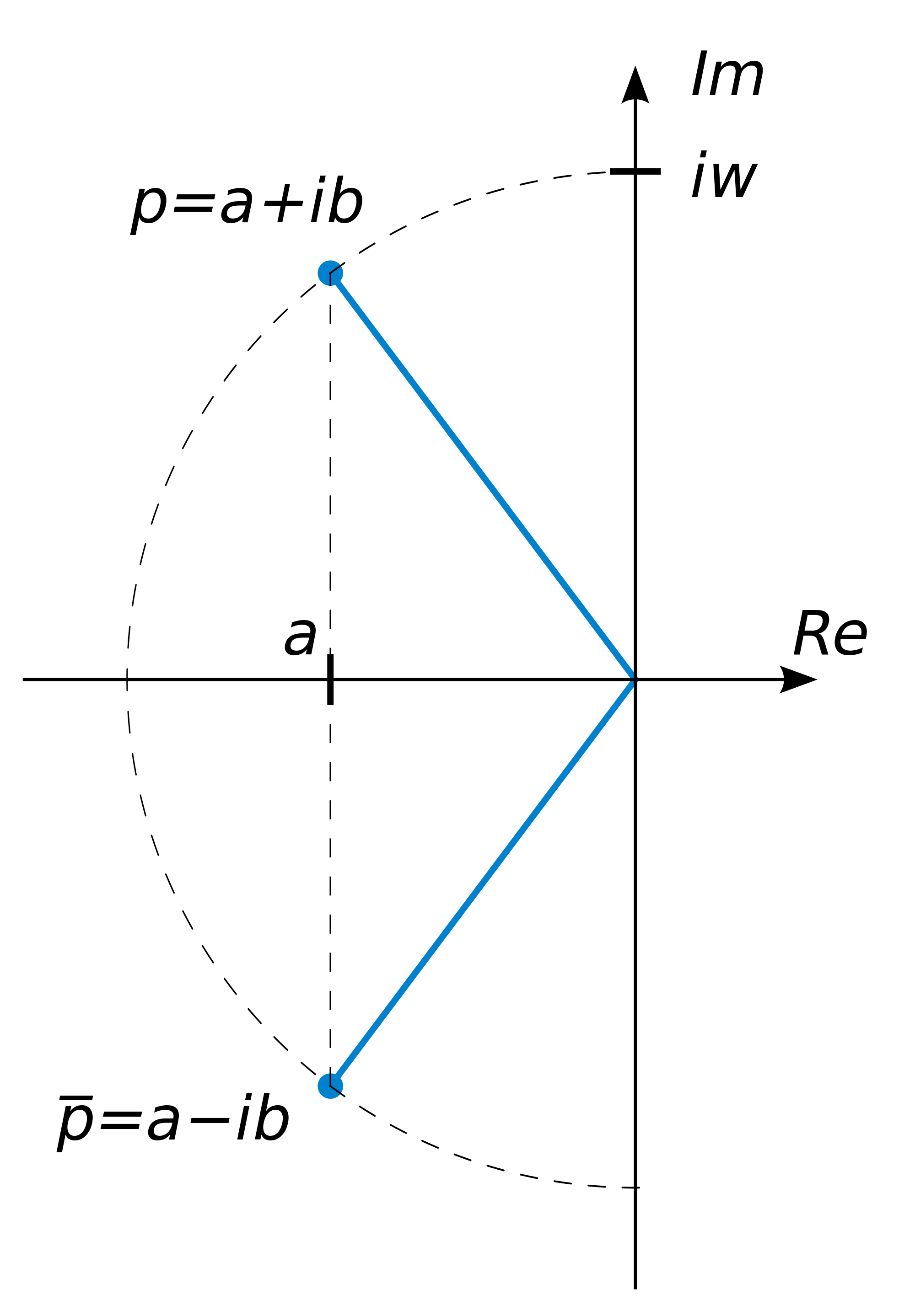
با توجه به تعریف فوق می‌توان دریافت که اعداد حقیقی دارای مزدوج مختلطی برابر با خودشان ‌می‌باشند، زیرا هر عدد حقیقی a را می‌توان به صورت زیر نمایش داد:

$ p = a+i0 $

چون در عبارت فوق، قسمت موهومی صفر است، لذا مزدوج مختلط این عدد هیچ تغییری نمی‌کند. پس داریم:

 $ \overline {p} = p $ 

پس در نهايت نكته زير را خواهيم داشت:

نکته ۱. هر عددی که خودش با مزدوجش برابر باشد، حتما یک عدد حقیقی است.

مثال۱. مزدج مختلط اعداد زیر را بدست آورید.

اگر ضرب و تقسیم اعداد مختلط را نمی‌دانید، این صفحه را مطالعه کنید. 

۱. $ z=a+2i   ⇒\overline{z}= a - 2i$

۲. $z=3i ⇒ \overline{z}=-3i$

۳. $z=(i+1)(5i+2)=(2-5)+i(2+5) ⇒ \overline{z}=-3-7i$

۴. $z=2(i+1) ⇒ \overline{z}= -2i+2$

۵. $z=\frac{2i+1}{3i+5} =\frac{(2i+1)(5-3i)}{(5-3i)(5+3i)}= \frac{(5+6)+(10-3)i}{25+9}=\frac{11}{34} + \frac{7}{34}i ⇒ \overline{z}=\frac{11}{34} - \frac{7}{34}i$

تمرین ۱. مزدوج مختلط اعداد زیر را بدست آورید.

۱. $ \frac{ \overline {50+1}}{3i}$

۲. $\overline{2i(6i+1)}$

۳. $\overline {i(i+1)(2i+5)} $

در این بخش از سایت ریاضیات ایران می‌خواهیم ببینیم چگونه می‌توانیم از تبدیلات لاپلاس برای حل معادلات دیفرانسیل استفاده کنیم. تبدیلات بسیاری برای حل معادلات دیفرانسیل وجود دارند. تبدیلات لاپلاس و فوریه، احتمالاً از عمومی ترین تبدیلاتی هستند که در این زمینه به کار برده می‌شوند. همانگونه که در بخش های بعدی سایت ریاضیات ایران خواهیم دید، با استفاده از تبدیلات لاپلاس می‌توانیم یک معادلات دیفرانسیل را به یک معادله جبری تبدیل کنیم و در بسیاری از موارد می‌توانیم آن مسأله جبری را به راحتی حل کنیم. تبدیلات لاپلاس همچنین در حل مسائل مقدار اولیه ای که نمی توانیم با روش‌های قبلی حل کنیم، به کار برده می‌شود.