فبل از اینکه وارد مباحث پیشرفته تر در مورد توابع شویم، باید دستگاه مختصات دکارتی و ویژگی های آن را بشناسیم. زیرا معمولاً برای رسم توابع از دستگاه مختصات دکارتی استفاده می‌کنیم. اما دستگاه مختصات دکارتی چیست؟

تقریباً همه با دستگاه مختصات دکارتی در دوره دبیرستان آشنا شده ایم اما مرور دوباره ای بر این دستگاه خالی از لطف نیست.

در دوره ابتدایی با محور اعداد آشنا شدیم. آنجا دیدیم که محور اعداد یک محور افقی است که از دو سمت راست و چپ ادامه می بابد و نقطه ای را به عنوان صفر (مرکز) در نظر می گیریم. اعداد مثبت را در سمت راست و اعداد منفی را در سمت چپِ صفر به ترتیب قرار می دهیم. واحد یا اندازه ای که برای تعیین اعداد روی نمودار انتخاب می شود برای اعداد مثبت و اعداد منفی باید با هم یکسان باشد. (به این محور اصطلاحاً محور یک بعدی یا دستگاه یک بعدی می گویند.)

دستگاه مختصات دکارتی از دو محور اعداد تشکیل شده است که این دو محور در نقطه های صفر خود، بر هم عمود هستند.

محور افقی را محور xها () و محور عمودی را محور yها () می‌نامیم. به این ترتیب صفحه، چهار قسمت می‌شود که هر قسمت را یک ربع یا ناحیه می‌نامیم. محل برخورد دو محور را مبدأ مختصات می‌نامیم. از مبدأ به سمت راست، اعداد مثبت و به سمت چپ اعداد منفی قرار داده می‌شوند (درست مانند محور اعداد حقیقی). همچنین، از مبدأ به سمت بالا، اعداد مثبت و به سمت پایین اعداد منفی را قرار می‌دهیم. دقت داریم که واحدی که برای نشان دادن اعداد روی محور xها و yها انتخاب می‌شود باید با هم برابر باشد. شکل زیر را ببینید:

در ربع اول، هم xها و هم yها مثبت هستند. در ربع دوم، xها منفی و yها مثبتند، در ربع سوم هم xها و هم yها منفی هستند و در ربع چهارم xها مثبت و yها منفی هستند.

نمایش اعداد در دستگاه مختصات دکارتی:

هر زوج مرتب را می توان به صورت یک نقطه در صفحه مختصات دکارتی نمایش داد. مؤلفه‌ی اول را از روی محور xها و سپس مؤلفه‌ی دوم را از روی محور yها انتخاب می‌کنیم (دقت داریم که زوج مرتب از سمت چپ خوانده می‌شود.). مثلاً (2,4) به این معنی است که اگر از مبدأ مختصات، دو واحد در جهت مثبت محور xها پیش رویم (اگر علامت مؤلفه x مثبت باشد، در جهت راست حرکت می‌کنیم و اگر منفی باشد به سمت چپ) و سپس چهار واحد در جهت مثبت محور yها (یعنی به سمت بالا) حرکت کنیم به نقطه‌ی (2,4) می‌رسیم (اگر علامت مؤلفه y مثبت باشد، در به سمت بالا حرکت می‌کنیم و اگر منفی باشد به سمت پایین).

پس جدول زیر را خواهیم داشت:

ناحیه (ربع)	مولفه x	مولفه y	مثال	تصویر
اول	مثبت	مثبت
دوم	منفی	مثبت
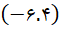سوم	منفی	منفی
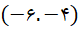چهارم	مثبت	منفی

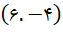مثال: نقاط (3,2) و 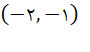 زیر را روی دستگاه مختصات دکارتی نمایش دهید:

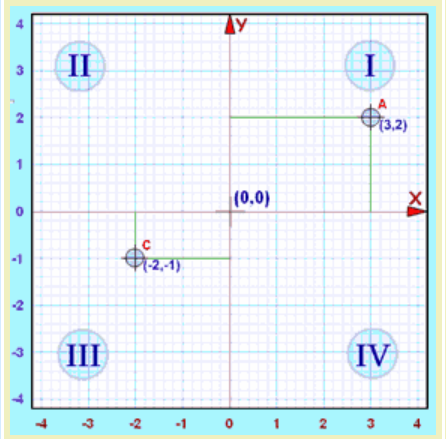
سؤال- در چه ربعی، xy مثبت است؟

می‌دانیم اگر حاصلضرب دو عدد مثبت باشد، باید دو عدد هم علامت باشند، یعنی یا هر دو مثبت باشند یا هر دو منفی. پس در ربع اول که هم x مثبت است و هم y، و ربع سوم که هم x منفی است هم y ، حاصلضرب x و y مثبت است یعنی داریم xy>0 .

رسم نمودار توابع

در درس قبل، دستگاه مختصات دکارتی را آموختیم و دیدیم که چگونه می‌توان زوج مرتب ها را در این دستگاه نشان داد. چون هر دوتایی مرتب فقط و فقط یک نقطه را در صفحه (دستگاه مختصات) تعیین می‌کند، از این پس می‌توانیم به آن نقطه بگوییم. همچنین دستگاه مختصات دکارتی دو بعدی را نیز می‌توانیم به عنوان یک صفحه در نظر بگیریم. به این ترتیب هر نقطه در این صفحه با دو مؤلفه تعیین می‌شود که به آن مختصات نقطه می گوییم . پس  برای مشخص شدن موقعیت نقطه در صفحه، مختصات آن لازم است.

نمودار تابع چیست؟

چون هر تابع، مجموعه‌ای از دوتایی های مرتب است، می‌توانیم آن‌ها را در دستگاه مختصات دکارتی نمایش دهیم. اگر بتوانیم تمام نقاط تابع را بر روی صفحه مشخص کنیم، شکلی به دست می‌آید که به آن نمودار تابع می‌گوییم. پس به صورت کلی، نمودار تابع مکان هندسی نقاطی از صفحه است که در ضابطه تابع صدق می‌کنند.

واضح است که رسم نمودار تابع به صورت کامل، در بسیاری از موارد امکان پذیر نیست، چون دامنه یا برد برخی توابع، همه اعداد حقیقی است و از هر دو جهت اعداد مثبت و منفی تا بینهایت ادامه دارند ولی صفحه‌هایی که ما در اختیار داریم، مانند صفحه کاغذ یا صفحه تبلت و ... محدود هستند. در این‌گونه موارد، بخشی از تابع را رسم می‌کنیم که نشان دهنده نمودار کلی آن تابع باشد. انتخاب مقیاس مناسب در رسم نمودارها نیز باید مورد توجه قرار گیرد. منظور این است که مقیاس به گونه ای انتخاب شود که نمودار نه آنقدر ریز باشد که جزئیات را نشان ندهد و نه آنقدر درشت باشد که بخش اصلی تابع را از دست بدهد. بدست آوردن دید درست از نمودارها و مقیاس مناسب، نیازمند تمرین و شناخت کافی از توابع است.

تابع ثابت

اکنون که با مفهوم تابع و نمودار تابع آشنا شدید، به معرفی توابع می‌پردازیم. در این درس در مورد تابع ثابت صحبت خواهیم کرد، ضابطه آن را خواهیم دید ، نمودار آن را رسم می‌کنیم و چند مثال خواهیم داشت.

آیا تا کنون ضرب المثل «حرف مرد یکی است» را شنیده‌اید؟ همیشه حرفش یکی است! یعنی هرچه شما بگویید، او فقط یک حرف می زند! تابع ثابت نیز چنین است! ببینید: