خانه

ترکیب ‎‏توابع:‎ فرض کنید که ‎‎$‎f:X‎\rightarrow ‎Y‎$‎‎‏ و ‎‎$‎g:Y‎\rightarrow ‎Z‎$‎‎‏ دو تابع باشند. ترکیب دو تابع f‎‎‎‎‏ و g‎ ‏‎ ‎تابعی‎ است که مقدار ‎‏‎‎$‎‎‎x\in D_f‎$‎‎ ‏را ‏به مقداری چون ‎$g(f(x))‎‎$‎ در‎‎‎ مجموعه ‎ Z‎‎‎می‌نگارد به این صورت که ابتدا تابع f روی x عمل می کند و خروجی $f(x)$ را تولید می‌کند سپس تابع g روی مقدار بدست آمده از تابع f عمل می کند و خروجی $g(f(x))$  را تولید می‌کند .‎‎ ترکیب دو تابع را با نماد ‎‎$gof‎$‎‎‏ یا $g(f(x))$ نشان می‌دهند.

‏شکل زیر کمک شایانی به درک هر چه بهتر این مفهوم خواهد نمود:

ساده ترین فرمول توابع را که به صورت $ f(x) = c $ بود را آموختیم و آن را تابع ثابت نام نهادیم و نمودار آن را رسم کردیم. در ادامه می خواهیم تابع های بیشتری را بیاموزیم و به مرور با تابع های پیچیده تر آشنا شویم. در این قسمت می خواهیم با خطوط راست در صفحه مختصات آشنا شویم، ضابطه آنها را بشناسیم، و چگونگی رسم نمودار آن‌ها را بیاموزیم.

ضابطه تابع خط راست: ضابطه تابع خط راست به صورت زیر است:

$ f(x) = ax + b $

در این فرمول $a$ و $b$ اعداد حقیقی هستند. دامنه و برد این تابع همه اعداد حقیقی ( $ \mathbb{R} $ ) است. مثلاً ضابطه‌های زیر، خط راست هستند:

$ f(x) = 2x + 1 $

$ f(x) = x - 1 $

$ f(x) = 0.5 x - 5 $

رسم نمودار خط راست: برای کشیدن نمودار هر خط راست، داشتن اطلاعات دو نقطه روی آن خط برای ما کافی است. برای این که دو نقطه روی خط به دست آوریم، باید دو مقدار دلخواه را برای x در نظر بگیریم و در فرمول تابع قرار داده تا مقدار $ y = f(x) $ متناظر آن به دست آید. سپس در صفحه مختصات، آن دو نقطه را پیدا می کنیم و با خط کش به هم وصل نموده و از دو طرف امتداد می دهیم. بیایید این کار را با مثال زیر دنبال کنیم:

مثال: نمودار تابع $ f(x) = 2x +1 $ را رسم کنید.

حل:  همان طور که گفتیم، دو مقدار برای x در نظر می گیریم:

$x = -1 $ و $ x = 2 $

این دو مقدار را در فرمول تابع قرار می دهیم و مقدار y متناظر هر کدام را به دست می آوریم:

$ x = 2 \Longrigharrow y = f(2) = 2 (2) +1 = 5 $

$ x = -1 \Longrightarrow y = f(-1) = 2 (-1) +1 = -1 $

پس دو نقطه $ A (2,5) $ و $ B(-1,-1) $ را داریم. اکنون این دو نقطه را روی صفحه مختصات پیدا می‌کنیم:

سپس دو نقطه را به هم وصل نموده و از دو طرف امتداد می دهیم :

سری تیلور چیست؟

سری تیلور یک چندجمله‌ای از درجه نامتناهی است و برای نمایش توابع مختلفی که خودشان چندجمله‌ای نیستند، استفاده می‌شود.

تعریف سری تیلور :

فرض کنید $ f(x) $ یک تابع حقیقی است که در نقطه $ x = a $‌ بی‌نهایت بار مشتق پذیر می‌باشد. سری تیلور تابع $ f(x) $  را در نقطه‌ی $ x = a $ به صورت زیر ارائه می‌دهد:

$ \sum_{n=0}^{\infty} f^{(n)} (a) \frac{(x-a)^{n}}{n!} = f(a) + f^{\prime} (a) (x-a) + f^{\prime\prime} (a) \frac{(x-a)^{2}}{2!} + f^{(3)} (a) \frac{(x-a)^{3}}{3!} + \cdots$

که به آن سری تیلور تابع $ f(x) $‌ در نقطه $ a $‌ می‌گوییم.

توجه داشته باشید که در فرمول بالا، $ f^{(n)} (a) $ به معنی مشتق  $ n $‌م تابع $ f(x) $  در نقطه‌ی $ x = a $ است.

روش محاسبه سری تیلور:

برای محاسبه سری تیلور یک تابع در نقطه داده شده، ابتدا مشتق تابع را گرفته و مقدار مشتق را در آن نقطه محاسبه می‌کنیم. سپس به ترتیب مشتق مرتبه دوم و سوم و ... را در نقطه داده شده محاسبه می کنیم. سپس مقادیر به دست آمده را در فرمول بالا جایگذاری کرده و بسط تیلور تابع به دست خواهد آمد.

اکنون با یک مثال به خوبی روش کار را ببینیم.

مثال: بسط تیلور تابع $ \cos x $ را حول نقطه $ x= \pi $‌ به دست آورید.

حل: در این مثال $ f(x) = \cos x $ و $ a = \pi $ . ابتدا مقدار تابع در این نقطه را محاسبه می کنیم و سپس مشتقات تابع را در این نقطه حساب می‌کنیم.

$ f(x) = \cos x \Longrightarrow f (\pi) = \cos (\pi) = -1 $

$ f(x) = \cos x \Longrightarrow f^{\prime} (x) = - \sin (x)  \Longrightarrow f^{\prime} (\pi) = - \sin (\pi) = 0 $

$ f^{\prime}(x) = - \sin (x) \Longrightarrow f^{\prime\prime} (x) = - \cos (x)  \Longrightarrow f^{\prime\prime} (\pi) = - \cos (\pi) = - (-1) = 1 $

$ f^{\prime\prime}(x) = - \cos (x) \Longrightarrow f^{(3)} (x) =  \sin (x)  \Longrightarrow f^{(3)} (\pi) =  \sin (\pi) = 0 $

$ f^{(3)}(x) = \sin (x) \Longrightarrow f^{(4)} (x) =  \cos (x)  \Longrightarrow f^{(4)} (\pi) =  \cos (\pi) = -1 $

و به همین ترتیب مشتق مراتب بالاتر در نقطه $ \pi $  به صورت زیر تکرار خواهد شد:

$  f^{(5)} (\pi) = 0  , f^{(6)} (\pi) = 1  , f^{(7)} (\pi) = 0  , f^{(8)} (\pi) = -1  , f^{(9)} (\pi) = 0  , \cdots  $

بنابراین سری تیلور تابع $ \cos x $ در نقطه $ x= \pi $‌ با جایگذاری مقادیر فوق در فرمول، به صورت زیر خواهد بود:

$ \begin{align*}  \sum_{n=0}^{\infty} f^{(n)} (\pi) \frac{(x-\pi)^{n}}{n!} &= f(\pi) + f^{\prime} (\pi) (x-\pi) + f^{\prime\prime} (\pi) \frac{(x-\pi)^{2}}{2!}  + f^{(3)} (\pi) \frac{(x-\pi)^{3}}{3!} + \cdots \\  &= -1 +  (0) (x-\pi) + 1\times \frac{(x-\pi)^{2}}{2!}  + 0 \times \frac{(x-\pi)^{3}}{3!} - 1 \times \frac{(x-\pi)^{4}}{4!} + 0 \times \frac{(x-\pi)^{5}}{5!} \\ & \qquad + 1 \times \frac{(x-\pi)^{6}}{6!} + 0 \times \frac{(x-\pi)^{7}}{7!} - 1 \times \frac{(x-\pi)^{8}}{8!} + 0 \times \frac{(x-\pi)^{9}}{9!} + \cdots  \\ & = -1 +\frac{(x-\pi)^{2}}{2!} -  \frac{(x-\pi)^{4}}{4!} + \frac{(x-\pi)^{6}}{6!} -\frac{(x-\pi)^{8}}{8!} + \cdots \\ & = -1 +\frac{1}{2!} (x-\pi)^{2} -  \frac{1}{4!} (x-\pi)^{4}+ \frac{1}{6!} (x-\pi)^{6} -\frac{1}{8!} (x-\pi)^{8} + \cdots \end{align*} $

این چندجمله‌ای سری تیلور تابع $ \cos x $ حول نقطه $ x= \pi $‌ می‌باشد. هرچه تعداد مراتب مشتق را بیشتر کنیم، دقت تخمین سری بیشتر خواهد شد و منحنی چندجمله‌ای بر منحنی تابع منطبق‌تر خواهد شد.

در شکل زیر شما نمودار سری‌های تیلور برای تابع $ \cos x $ در نقطه $ x= 0 $‌ نمایش داده شده است. هرچه تعداد جملات بیشتری را انتخاب کنیم، تطابق دو منحنی بر هم بیشتر خواهد شد.

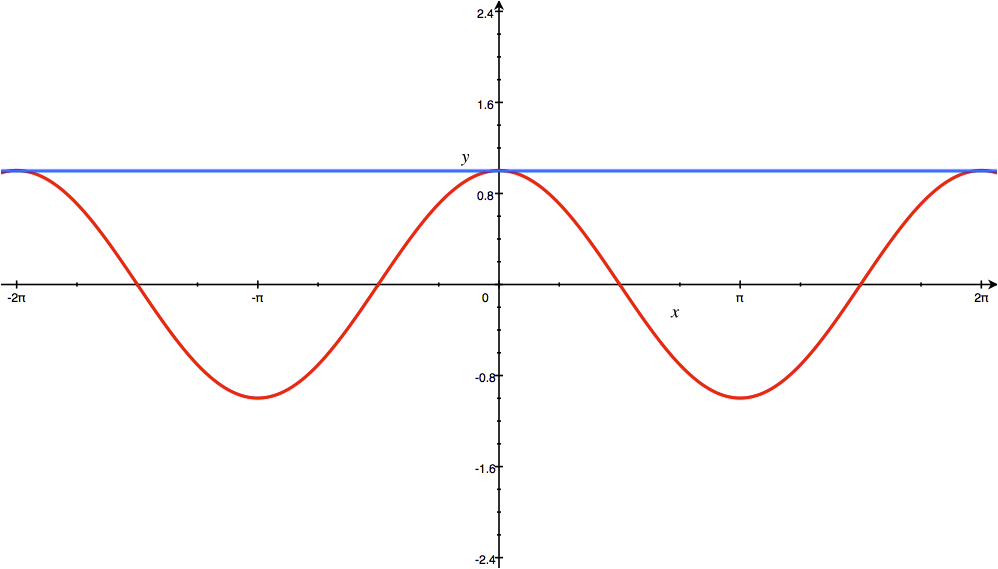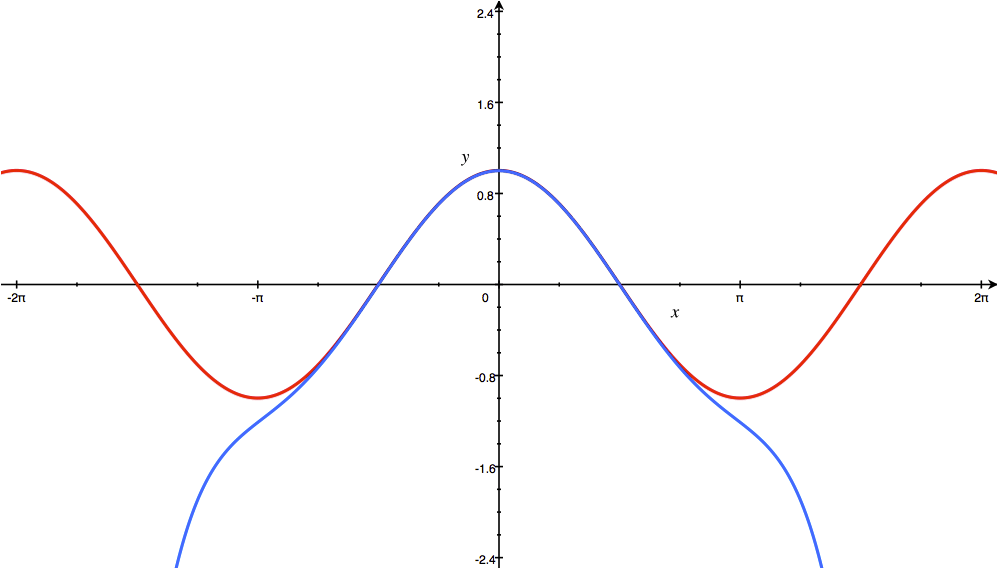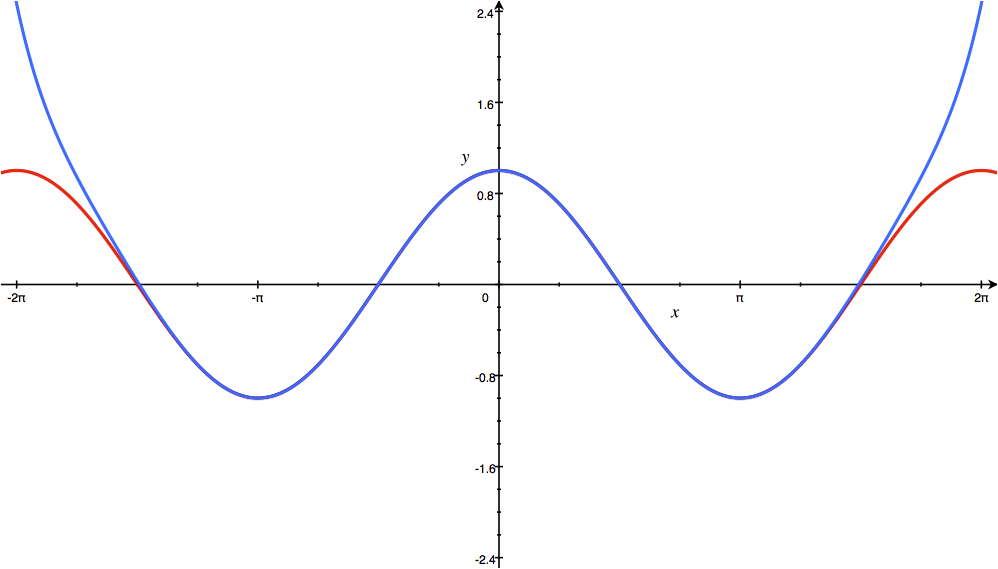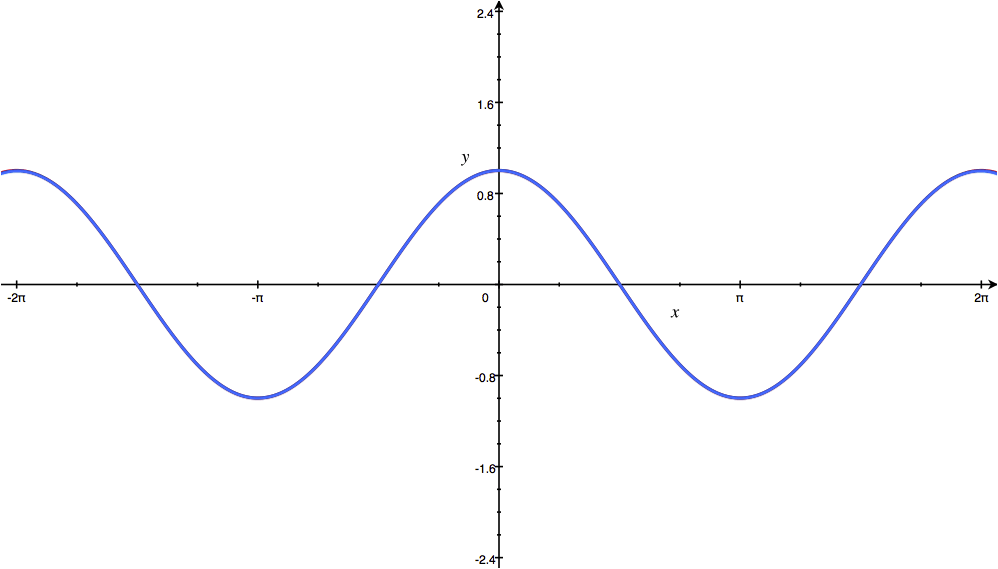
 حالا شما سری تیلور تابع $ \cos x $ در نقطه $ x= 0 $‌ را محاسبه کنید و با شکل بالا آن را مقایسه کنید.

تمرین ۱: سری تیلور تابع $ f(x) = e^{x} $ در نقطه $ x= 0 $‌ بیابید.

تمرین ۲: سری تیلور تابع $ f(x) = \sin x $ در نقطه $ x= 0 $‌ بیابید.