خانه
تعریف تبدیل لاپلاس با مثال های متنوع
تبدیل لاپلاس
در این درس از سایت ریاضیات ایران، تبدیل لاپلاس را معرفی نموده و با شش مثال مهم و یک تمرین، درس را ادامه می دهیم. قبل از این که به ارائه تعریف لاپلاس بپردازیم، باید تعریف دیگری را به عنوان مقدمه ذکر کنیم.
تعریف1: تابع قطعهای پیوسته
یک تابع، روی یک بازه، قطعهای پیوسته نامیده میشود، اگر بتوان بازه را به تعداد متناهی زیربازه، که تابع روی آن زیربازه های باز، پیوسته است و در نقاط انتهایی هر زیربازه، دارای حد متناهی است، تقسیم کرد.
در زیر نمودار یک تابع قطعهای پیوسته را مشاهده میکنید.
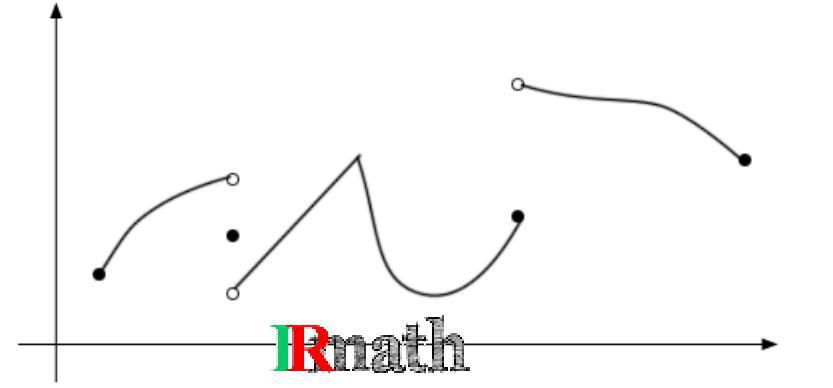
به عبارت دیگر، یک تابع قطعهای پیوسته، تابعی است که در تعداد متناهی نقطه جدا شده است ولی در هیچ جایی به بی نهایت نمیگراید.
اکنون میتوانیم تعریف تبدیل لاپلاس را داشته باشیم:
تعریف تبدیل لاپلاس:
فرض کنید ![]() تابعی قطعهای پیوسته باشد، تبدیل لاپلاسِ
تابعی قطعهای پیوسته باشد، تبدیل لاپلاسِ ![]() را با
را با ![]() نمایش میدهیم و به صورت زیر تعریف میکنیم:
نمایش میدهیم و به صورت زیر تعریف میکنیم:
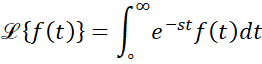
مرسوم است که لاپلاس تابع ![]() یعنی
یعنی ![]() را با نماد
را با نماد ![]() نمایش دهند.
نمایش دهند.
در ادامه مطلب شش مثال متنوع و مفید در به دست آوردن تبدیلات لاپلاس ارائه می کنیم که با این مثال ها شما با اصول اولیه کار و محاسبه تبدیلات لاپلاس آشنا می شوید.
ریاضی, معادلات دیفرانسیل, لاپلاس
- بازدید: 32629
جدول تبدیلات لاپلاس
جدول تبدیلات لاپلاس
جدول تبدیلات لاپلاس شامل تابعهای مهم و تبدیل لاپلاس آنها میباشد. تبدیلات لاپلاس بسیاری از توابع مهم (۳۷ نوع تابع) در سایت ریاضیات ایران محاسبه شده و فرمول نهایی آن در این جدول آورده شده است. پیشنهاد میگردد تبدیلات لاپلاس این جدول را به خاطر بسپارید و در مواقع لزوم از آنها برای محاسبه تبدیلات لاپلاس توابع پیچیده تر استفاده نمایید. سعی شده است تبدیل لاپلاس بسیاری از توابعی که عموماً مورد نیاز است در این جدول آورده شود، به همین جهت کاملترین جدول تبدیلات لاپلاس میباشد. اما بدون شک تبدیل لاپلاس همه توابع در آن نیست.
- بازدید: 96897
تبدیل لاپلاس ترکیب خطی توابع
تبدیل لاپلاس ترکیب خطی توابع
همانگونه که در درس اول تبدیلات لاپلاس در سایت ریاضیات ایران مشاهده نمودید، محاسبه مستقیم تبدیلات لاپلاس کاری واقعاً پیچیده است. معمولاً هنگام محاسبه واقعی تبدیلات لاپلاس، از جدول تبدیلات لاپلاس استفاده میکنیم. جدولی که شامل تبدیلات لاپلاس توابع عمومی و مهم است و بسیاری از تبدیلات لاپلاس خواسته شده را میتوان از این جدول با اندکی تغییر به دست آورد.
اولین قضیه ای که در محاسبه تبدیلات لاپلاس از آن میتوانیم استفاده کنیم «قضیهی لاپلاس ترکیب خطی دو تابع» است که به صورت زیر بیان می شود:
قضیه تبدیل لاپلاس ترکیب خطی دو تابع: فرض کنید f(t) و g(t) دو تابع باشند که تبدیلات لاپلاس آنها را میدانیم یا در جدول تبدیلات لاپلاس موجود باشد و a و b دو عدد حقیقی دلخواه باشند، در این صورت تبدیلات لاپلاس ترکیب خطی f و g یعنی ![]() به صورت زیر محاسبه میشود:
به صورت زیر محاسبه میشود:
![]()
یا به طور خلاصه اگر ![]() و
و ![]() باشد، داریم:
باشد، داریم:
![]()
به بیان دیگر، ما نگران ضرب و تقسیم عدد در یک تابع و حتی جمع و تفریق توابع نیستیم. در این حالتها میتوانیم همان عملیات را روی تبدیلات لاپلاس نظیر نیز انجام دهیم. مثالهای زیر را ببینید.
- بازدید: 13167
معکوس تبدیل لاپلاس
معکوس تبدیل لاپلاس
یافتن تبدیل لاپلاس یک تابع با داشتن جدول تبدیلات لاپلاس که در بخش های قبل سایت ریاضیات ایران دیدید، کار پیچیده ای نیست. در این درس میخواهیم ببینیم اگر یک تبدیل لاپلاس داده شده باشد، میتوانیم تابع یا تابعهای اولیه این تبدیل را بیاییم یا خیر؟ همانطور که خواهیم دید این کار امکانپذیر است ولی کمی پیچیده تر از محاسبه تبدیل لاپلاس است.
در این حالت میگوییم تبدیل معکوس لاپلاس ![]() را مییابیم و از نوشتار زیر استفاده میکنیم :
را مییابیم و از نوشتار زیر استفاده میکنیم :
![]()
- بازدید: 29785