خانه
معکوس رابطه
معکوس رابطه: فرض کنید که رابطه f از مجموعه A به مجموعه B به صورت زیر بیان شده باشد:
$f =\{(a , b) \subset A\times B | a\in A , b\in B \}$
در اینصورت رابطه g از مجموعه B به مجموعه A را معکوس رابطه f گویند، هرگاه g به شکل زیر بیان گردد:
$g=\{(b , a) \subset B\times A |(a , b)\in f \}$
معکوس رابطه f را میتوان با نماد g=f-1 نشان داد.
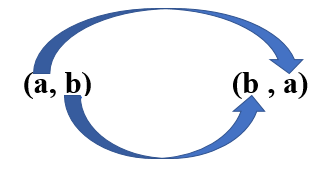
در واقع تعریف بالا میگوید، با جابهجایی مولفه های تمام زوجهای مرتب ((a , b در داخل مجموعه f میتوانید معکوس یک رابطه را به دست آورید.
- بازدید: 9691
معکوس تابع
با توجه به این که هر تابع خود نیز یک رابطه است، تعریف زیر را نیز برای معکوس یک تابع میتوان بیان نمود:
معکوس تابع : تابع f که از مجموعه A (دامنه تابع) به مجموعه B (برد تابع) به صورت زیر بیان شده است، را در نظر بگیرید.
$f: A\rightarrow B$
$f =\{(a , b) \subset A\times B | a\in A , b\in B \}$
در اینصورت معکوس تابع f، رابطهای چونg است که به شکل زیر خواهد بود:
$ f: B\rightarrow A$
$g=\{(b , a) \subset B\times A |(a , b)\in f \}$
معکوس تابع f را نیز با نماد f-1 نشان میدهیم.
در واقع تعریف بالا بیان میکند، تابع معکوس را میتوان با جابهجا کردن مکان مولفههای تمام زوجهای مرتبی که در مجموعه f موجود میباشند به دست آورد.
مثال ۱. معکوس توابع زیر را به دست آورید.
- $f =\{(1 , 5) , (2 , 6), (3 , 4)\}$
معکوس تابع f به صورت زیر بدست خواهد آمد:
$f^{-1} =\{(5 , 1) , (2 , 6), (4 , 3) \}$
با توجه به شکل زیر میتوان مشاهده کرد که برای به دست آوردن معکوس تابع f کافی است جای مولفه های هر زوج مرتب در مجموعه f را عوض کنید.
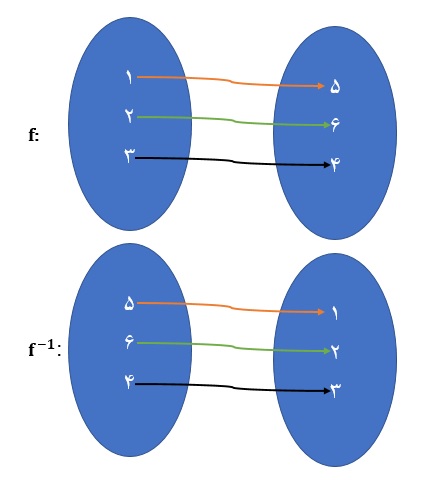
در قسمت اول این مثال مشاهده میکنید که معکوس تابع f ، خود نیز یک تابع است.
- $g =\{(1 ,a) , (2 , a), (3 , 4)\}$
داریم:
$g^{-1} =\{(a , 1) , (a , 2), (3 , 4)\}$
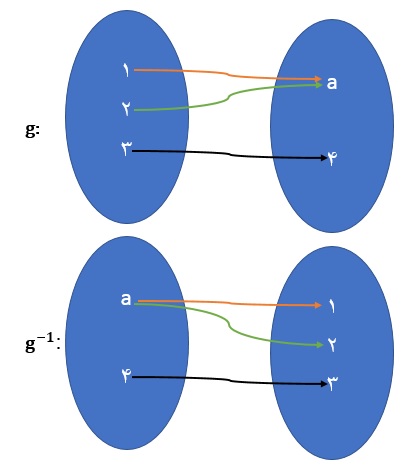
قسمت دوم مثال بالا نشان میدهد که معکوس تابع g تنها یک رابطه است و تابع نمیباشد، زیرا پیکان مربوط به عنصر a در 1-g به دو عضو ۱ و ۲ متصل شده است و این موضوع در تناقض با مفهوم تابع بودن میباشد. اکنون سوالی که در اینجا مطرح میگردد این است که در چه شرایطی معکوس یک تابع، خود نیز یک تابع است؟ برای پاسخ به این سوال میتوانید به مفهوم یک به یک بودن رجوع نمایید.
نکته ۱. با توجه به مثال بالا میتوان بیان نمود که معکوس یک تابع لزوماً تابع نیست.
تمرین ۱. معکوس توابع زیر را به دست آورید و با رسم شکل نشان دهید معکوس کدامیک تابع و معکوس کدامیک تنها یک رابطه است.
- $f = \{(1 , 1) , (5 , a) , (6 , 3) , (c , d) \}$
- $g =\{( 6 , 3), (a , a) , (10 , 1) , (11 , 1) , (12 , a) \}$
- $h = \{(xx , x) , (xxx , x) , (x , x) \}$
ریاضی, مجموعه, رابطه, تابع, معکوس تابع, دوتایی مرتب (زوج مرتب)
- بازدید: 7844
تابع یک به یک، روش تشخیص، مثال و تمرین
تابع یک به یک: فرض کنید f تابعی از مجموعه A به مجموعه B باشد. هرگاه تصویر هر عضو از مجموعه A تنها یک عضو منحصر به فرد در مجموعه B باشد. در اینصورت تابع f را یک به یک گویند. این تعریف را میتوان با استفاده از نمادهای ریاضی به گونه زیر بیان نمود:
$\forall a , b\in A, \:\: if\: \: f(a) =f(b)\rightarrow a=b$
در واقع عبارت فوق بیان میکند، هر زمان تصویر تابع (خروجی تابع) یک به یک f در دو نقطه از دامنه مساوی باشد حتماً آن دو نقطه دارای مقدار یکسان خواهند بود.
ریاضی, مجموعه, تابع, یک به یک, دوتایی مرتب (زوج مرتب)
- بازدید: 102085
تابع پوشا، تعریف، مثال و تمرین
تابع پوشا: تابع f از مجموعه A به B را در نظر بگیرید. هرگاه به ازای هر عضو b از مجموعه B حداقل یک عضو a در مجموعه A موجود باشد به گونهای که داشته باشیم
$f(a) = b$
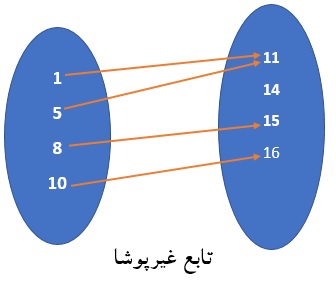
در اینصورت تابع f را پوشا گویند. با توجه به تعریف همچنین میتوان گفت زمانی یک تابع غیرپوشاست که بتوان عنصری در برد تابع یافت که تصویر هیچ عنصری از عناصر دامنه تابع نباشد. با توجه به اشکال زیر میتوان این مفاهیم را بهتر درک نمود:
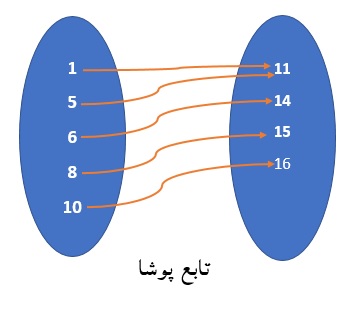
از تعریف بالا این موضوع نتیجه میشود، زمانی که یک تابع پوشاست رابطه زیر بین دامنه و برد یک تابع برقرار خواهد شد:
$f(D_f) = R_f$
که در آن $D_f$ و $R_f$ به ترتیب دامنه و برد تابع f میباشند که به صورت زیر تعریف میشوند:
$D_f=\{x\in A | f(x) \in B \} \subset A$
$R_f =\{ f(x) \in B| x\in D_f \} \subset B$
همچنین پوشا بودن تابع $f:A \rightarrow B$ را میتوان با استفاده از نمادهای ریاضی به گونه زیر بیان نمود:
$\forall y\in R_f, \exists x\in D_f \rightarrow f(x) =y$
در واقع با توجه به عبارت بالا شما میتوانید پوشا بودن یک تابع را مورد بررسی قرار دهید.
نکته : دقت کنید که پوشا بودن یک تابع را نمیتوان از روی نمودار، مشابه کاری که برای بررسی یک به یک بودن و تابع بودن از روی نمودار صورت میگرفت به دست آورد. برای بررسی پوشا بودن از تعریف ریاضی آن اقدام نمایید. مثالهای زیر نحوه بررسی نمودن این موضوع را نشان خواهد داد.
مثال : کدامیک از توابع زیر پوشا میباشند.
$f(x) = x+1$
برای بررسی پوشایی تابع f، ابتدا yای دلخواه را از برد تابع f در نظر میگیریم، حال اگر بتوانیم xای را از دامنه تابع f پیدا کنیم به گونه ای که $f(x)= y$ باشد پوشایی تابع مورد نظر را ثابت نمودهایم.
$\forall y \in R_f , \exists x\in D_f \rightarrow f(x) =x+1=y$
حال کافی است از عبارت بالا، xای را بر حسب y محاسبه کنیم. در صورتی که بتوانیم چنین xای را در دامنه تابع f بیابیم لذا تابع f پوشا خواهد بود.
⇒ $y=x+1 \rightarrow x=y+1$
در نتیجه کافی است برای هر yای دلخواه از برد تابع، x را مساوی با عبارت y+1 در نظر بگیریم. از آنجا که دامنه و برد تابع $\mathcal{R}$ میباشند لذا عبارت یافته شده برای x عضوی از دامنه خواهد بود و تابع مورد نظر پوشاست.
$g(x)=x^2, \: D_g, R_g=\mathcal{R}$
با توجه به دامنه و بردی که تابع g دارد میتوان دریافت که تابع g تابعی پوشانیست، زیرا به ازای اعداد منفی همچون 1- در برد تابع g، نمیتوان xای از دامنه به دست آورد که $x^2= -1$ شود. لذا تابع g پوشا نخواهد بود. اما اگر برد تابع g را از $\mathcal{R}$ به بازهی $[0 , \infty)$ محدود کنیم آنگاه تابع g پوشا خواهد شد. برای بررسی پوشایی تابع g با شرط گفته شده مشابه کاری که برای تابع f صورت گرفت اقدام میکنیم. داریم:
$\forall y \in [0 , \infty), \exists x\in \mathcal{R} \rightarrow f(x)= x^2=y$ ⇒ $x= ± \sqrt{y}$
در نتیجه توانستیم به ازای هر yای که از برد تابع g در نظر میگیریم حداقل یک xای از دامنه را بیابیم لذا تابع g پوشاست.
تمرین ۱. کدامیک از یک توابع زیر پوشا هستید در صورت غیرپوشایی آیا میتوان با تحدید دامنه یا برد آن را پوشا نمود؟
$f(x)= x^3 +x, D_f , R_f = R$
$g(x)= \sqrt{x}, D_g , R_g= [0 , \infty)$
$h(x) = \frac{x^2 + 1}{x^ +3} , D_h , R_h= R$
- بازدید: 41530