خانه
دترمینان
تعریف دترمینان: فرض کنید که $A = [a_{ij}]$ یک ماتریس مربعی از مرتبه $n$ به صورت زیر باشد:
$A=\begin{bmatrix}a_{11}&a_{12}&.&.&.&a_{1n}\\.&.&.&.&.&.\\.&&&&&.\\.&&&&&.\\.&&&&&.\\a_{n1}&a_{n2}&.&.&.&a_{nn}\end{bmatrix}$
ابتدا یادآوری کنیم که نمایش ماتریس $A$ به صورت بردارهای ستونی به شکل زیر خواهد بود:
$\begin{bmatrix}a_1 & .&.&. & a_n \end{bmatrix}$
که $a_j$ ستون jم ماتریس میباشد. یعنی به ازای $1 \leq j \leq n$ برداری از مرتبه $n \times 1$ داریم:
$a_{j}=\begin{bmatrix}a_{1j} \\ a_{2j} \\ . \\. \\. \\ a_{nj}\end{bmatrix}$
در این صورت دترمینان ماتریس $A$ را به صورت زیر تعریف میکنیم:
$det(A) = \sum_{\sigma \in S_n} (sgn( \sigma) \prod_{i=1}^n a_{i , \sigma_i})$
و به صورت $ det(A) = \left| A \right| $ نشان میدهیم.
در واقع فرمول بالا مجموع را بر روی تمام جایگشتهای $\sigma$ از مجموعه $\{ 1 ... , n \}$ محاسبه میکند. نماد $\prod_{i=1}^n a_i , \sigma_i$ در واقع حاصلضرب $a_{1,\sigma_1}\times a_{2,\sigma_2}...\times a_{n,\sigma_n}$ را نشان میدهد.
مثال ۱. فرض کنید که $A = \begin{bmatrix}1 & 2 \\3 & 5 \end{bmatrix}$ باشد. دترمینان ماتریس $A$ را محاسبه کنید.
چون $A$ یک ماتریس $2 \times 2$ میباشد. پس $S = \{ 1, 2 \}$ در نظر گرفته و تمام جایگشتهای آن به صورت زیر خواهد بود:
$S_2 = \{ \alpha = \begin{pmatrix}1 & 2 \\1 & 2 \end{pmatrix} , \beta = \begin{pmatrix}1 & 2 \\2 & 1 \end{pmatrix} \}$
دترمینان این ماتریس با توجه به تعریف دترمینان به صورت زیر به دست خواهد آمد:
$det(A) = det (\begin{bmatrix}1 &2 \\3 &5 \end{bmatrix}) = \sum_{\sigma \in S_2} sgn(\sigma) a_{1 , \sigma(1)}a_{2 , \sigma(2)} = sgn(\alpha) a_{1 , \alpha (1)} a_{2 , \alpha (2)} + sgn ( \beta) a_{1 , \beta(1)} a_{2 , \beta(2)}$
حال با توجه به مفاهیم جایگشتهای زوج و فرد داریم:
$sgn(\alpha) =1,\:\:\: sgn( \beta) = -1$
و از طرفی داریم:
$\alpha(1) = 1 ,\:\: \alpha(2) = 2$
$\beta(1) = 2 ,\:\: \beta(2) = 1$
پس در نتیجه دترمینان این ماتریس برابر خواهد بود با
$det(A) = 1 \times a_{11} a_{22} + (-1) \times a_{12}a_{22} = 1 \times 1 \times 5 - 2 \times 3 = 5 -6 = -1$
نکته ۱. $A = \begin{bmatrix}a_{11} & a_{12} \\a_{21} & a_{22} \end{bmatrix}$ یک ماتریس از مرتبه $ 2 \times 2$ باشد. در این صورت با توجه به تعریف دترمینان، مقدار دترمینان ماتریس $2 \times 2$ برابر خواهد شد با
$det(A) = a_{11}a_{22} - a_{12}a_{21}$
تمرین ۱. دترمینان ماتریس $3 \times 3$ زیر را محاسبه کنید:
$\begin{bmatrix}a_{11} & a_{12} & a_{13} \\a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{bmatrix}$
تمرین ۲. دترمینان ماتریسهای زیر را محاسبه کنید.
۱. $A = \begin{bmatrix}1 & 5 & 7 \\8 & 9 & 0 \\ 1 & 0 & 0 \end{bmatrix}$
۲. $B = \begin{bmatrix}1 & 5 & 3 \\2 & 1 & 4 \\ 7 & 8 & 9 \end{bmatrix}$
۳. $C = \begin{bmatrix}1 & 5 \\0 & 3 \end{bmatrix}$
ریاضی, ماتریس, جبرخطی, دترمینان
- بازدید: 2501
ضرب نقطهای یا اسکالری یا داخلی دو بردار
تعریف ضرب نقطهای دو بردار: فرض کنید که $\overrightarrow{a} = (a_1 , ... , a_n)$ و $\overrightarrow{b} = (b_1 , ... , b_n)$ دو بردار از مرتبه $n$ باشند. در اینصورت ضرب نقطهای دو بردار $ \overrightarrow{a} $ و $\overrightarrow{b} $ به صورت زیر تعریف میکنیم:
$\overrightarrow{a} . \overrightarrow{b} = a_1 . b_1 + a_2 . b_2 + ... + a_n . b_n = \sum _{i = 1} ^n a_i . b_i$
در واقع عبارت بالا میگوید که ضرب نقطهای دو بردار $ \overrightarrow{a} $ و $ \overrightarrow{b} $ برابر با مجموع ضرب درایههای متناظر آن دو بردار میباشد.
ضرب نقطه ای را ضرب اسکالر دو بردار یا ضرب داخلی دو بردار را نیز می گویند.
برای بردارهای مختط، ضرب نقطهای بین دو بردار به صورت زیر تعریف میشود:
$\overrightarrow{a} . \overrightarrow{b} = a_1 . \overline{b_1} + a_2 . \overline{b_2} + ... + a_n . \overline{b_n} = \sum _{i = 1} ^n a_i . \overline{b_i}$
که در آن $\overline{b_i}$ مزدوج مختلط $b_i$ خواهد بود.
نکته ۱. ضرب نقطهای بین دو بردار $ \overrightarrow{a}$ و $ \overrightarrow{b} $ را میتوان با استفاده از زاویه بین این دو بردار نیز به دست آورد. فرض کنید که $\theta$ زاویه بین دو بردار $ \overrightarrow{a} $ و $ \overrightarrow{b} $ باشد. در اینصورت ضرب نقطهای این دو بردار به شکل زیر به دست خواهد آمد:
$ \overrightarrow{a} . \overrightarrow{b} = || a || . ||b||cos \theta $
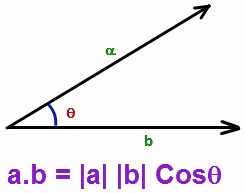
به بیان ساده تر، ضرب نقطه ای دو بردار برابر است با حاصلضرب طول بردارها در کسینوس زاویه بین آن ها.بنابراین برای محاسبه زاویه بین دو بردار نیز می توان از این رابطه استفاده کرد.
با استفاده از عبارت بالا میتوان حالتهای زیر را نتیجه گرفت:
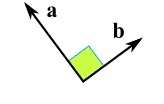
۱. زمانی که دو بردار عمود بر هم باشند، یعنی زاویه بین آنها ۹۰ درجه باشد. در اینصورت ضرب نقطهای این دو بردار چون $ \cos 90 = 0 $ است، مساوی صفر خواهد شد.
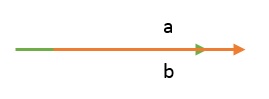
۲. زمانی که دو بردار در یک جهت هم راستا باشند. در اینصورت زاویه بین این دو بردار صفر خواهد بود و $ \cos 0 = 1 $ است. لذا داریم:
$ \overrightarrow{a} . \overrightarrow{b} = ||a|| . ||b|| $
نکته ۲ ارتباط بین طول یک بردار و ضرب نقطه ای. برای محاسبه اندازه یک بردار داریم:
$ \overrightarrow{a} . \overrightarrow{a} = ||a||^2 \Rightarrow ||a|| = \sqrt{ \overrightarrow{a} . \overrightarrow{a}} $
در واقع این عبارت برابر با طول اقلیدسی یک بردار خواهد بود. پس طول یک بردار برابر با جذر حاصلضرب نقطه ای بردار در خودش است.
مثال ۱. فرض کنید که $ \overrightarrow{a} $ و $ \overrightarrow{b} $ دو بردار باشند که به صورت زیر تعریف شدهاند. در اینصورت ضرب نقطهای دو بردار را محاسبه کنید.
$ \overrightarrow{a} , \overrightarrow{b} = ||a|| . ||b|| \cos \theta = ||a|| ||b|| \cos 30 = 5 \times 13 \cos 30 = 65 \frac {\sqrt{3}}{2}$
$ \overrightarrow{a} , \overrightarrow{b} = ||a|| . ||b|| \cos \theta = 10 \times 15 \cos \frac{4 \pi}{6} = 10 \times 15 \cos \frac{4 \pi}{6} = 150 \cos \frac{4 \pi}{6}$
مثال ۲. ضرب نقطهای بردارهای زیر را محاسبه کنید
۱. $ \overrightarrow{a} = ( 1 , i , 2) , \overrightarrow{b} = (2 , 0 , i+1) $
چون مولفههای بردار مختلط هستند، داریم:
$ \overrightarrow{a} .\overrightarrow{b} = 1 \times \overline{2} + i \times \overline{0} + 2 \times (\overline{i+1}) = 2 + 0 + 2(1-i) = 2 + 2 -2i = 4-2i $
۲. $ \overrightarrow{a} = ( 5,3) , \overrightarrow{b} = (7,1)$
$ \overrightarrow{a} . \overrightarrow{b} = (5,3).(7,1) = 35+3 = 38$
مثال ۳. فرض کنید که دو بردار $ \overrightarrow{a} $ و $ \overrightarrow{b} $ دارای اندازههای ۵ و ۱۰ باشند. ضرب نقطهای این دو بردار برابر با ۳۵ باشد. در اینصورت زاویه بین این دو بردار را محاسبه کنید.
$ \overrightarrow{a} . \overrightarrow{b} = || a || . ||b||\cos \theta $
با استفاده از این فرمول داریم:
$ 35 = 10 \times 5 cos \theta \Rightarrow \frac{35}{50} = \cos \theta \Rightarrow \frac{7}{10} = \theta = \cos^{-1}(0.7) $
تمرین ۱. ضرب داخلی بین دو بردارهای $ \overrightarrow{a}$ و $\overrightarrow{b} $ را محاسبه کنید.
$\overrightarrow{a} = (5i , 1+i , 2i)$
$\overrightarrow{b} = (3i , 2i , 1)$
تمرین ۲. زاویه بین دو بردار $ \overrightarrow{a} $ و $ \overrightarrow{b} $ زمانی که اندازه $ \overrightarrow{a} =3 $ و $ \overrightarrow{b} = 5 $ میباشد و ضرب نقطهای بین آنها $\overline{30}$ است را محاسبه کنید.
- بازدید: 34453
بردار یکه و بردار جهت یک بردار
تعریف بردار یکه: هر بردار با طول واحد (یک) را بردار یکه میگوییم.
تعریف بردار جهت: بردار یکهای که موازی و هم جهت با بردار $a$ باشد، بردار جهت $a$ گویند. بردار جهت $a$ را با نماد $e_a$ نمایش میدهند و از رابطه زیر به دست میآورند:
$ e_a = \frac {1}{ |a|} \overrightarrow{a}$
که در آن $|a|$ نشان دهندهی اندازه (طول) بردار a میباشد.
یادآوری: اگر بردار a یک بردار سه بعدی به صورت $ a = (a_x , a_y , a_z)$ باشد، طول آن به صورت زیر محاسبه میشود:
$|a| = \sqrt { a_{x}^2 + a_{y}^2 + a_{z}^2}$
پس به طور خلاصه هر بردار، با یک کمیت عددی غیر منفی $|a|$ که طول آن است و یک بردار یکه $e_a$ که جهت آن را تعیین میکند، مشخص میشود. یعنی داریم:
$ a = | \alpha|{e_a}$
بردارهای یکهای که در راستای محورهای مختصات باشند، را بردارهای یکه مختصات گویند. در فضای سه بعدی بردارهای یکه عبارتند از:
$\overrightarrow{i}$ بردار یکه در راستای محور x مختصات.
$\overrightarrow{j}$ بردار یکه در راستای محور y مختصات.
$\overrightarrow{k}$ بردار یکه در راستای محور z مختصات.
هر بردار دلخواه در فضای سه بعدی را میتوان بر حسب این بردارهای یکه نمایش داد.
فرض کنید که $\overrightarrow{a} = (a_x, a_y, a_z)$ برداری در فضای سه بعدی باشد. در اینصورت داریم:
$\overrightarrow{a} = a_x \overrightarrow{i} + a_y \overrightarrow{j} + a_z \overrightarrow{k}$
مثال ۱. بردارهای زیر را برحسب بردارهای یکه نمایش دهید.
۱. $\overrightarrow{a} = (1,2,3) \rightarrow \overrightarrow{a} = \overrightarrow{i} + 2 \overrightarrow{j} + 3 \overrightarrow{k}$
۲. $ \overrightarrow{b} = (5,6,7) \rightarrow \overrightarrow{b} = 5\overrightarrow{i} + 6 \overrightarrow{j} + 7 \overrightarrow{k}$
۳. $\overrightarrow{c} = (0,1,0) \rightarrow \overrightarrow{c} = 0\overrightarrow{i} + 1 \overrightarrow{j} + 0 \overrightarrow{k}$
تمرین ۱. بردارهای زیر را برحسب بردارهای یکه مختصات نمایش دهید.
۱. $ \overrightarrow{a} = (5,0,2) $
۲. $ \overrightarrow{b} = (3,1,2) $
۳. $ ea+2b $
۴. $e_{2b} $
۵. $e_{3a}$
۶. $e_a +7b$
- بازدید: 37650
دو بردار متعامد
تعریف دو بردار متعامد: فرض کنید که x و y دو بردار در فضای ضرب داخلی $V$ باشند. دو بردار x و y را متعامد گویند، هرگاه ضرب داخلی بین این دو بردار برابر صفر شود، یعنی
$<x,y> = 0$
وقتی دو بردار با یکدیگر متعامد هستند، آن را با نماد $x \bot y$ نمایش میدهند.
مثال ۱. آیا دو بردار $ (0,5,1) $ و $ (1,0,0)$ متعامد هستند؟
برای اثبات تعامد بین این دو بردار در فضای $ \mathbb{R}^3$ به گونه زیر عمل میکنیم:
در ابتدا ضرب داخلی تعریف شده بر فضای $\mathbb{R}^3$ را برای دو بردار $a=(a_1 , a_2 , a_3)$ و $b=(b_1 , b_2, b_3)$ به صورت زیر بیان میکنیم:
$<a , b>= a_1 . b_1 + a_2 . b_2 + a_3 . b_3$
با توجه به تعریف ضرب داخلی شرط متعامد بودن دو بردار را بررسی میکنیم. لذا داریم:
$(1,0,0).(0,5,1) = 1 \times 0 + 0 \times 5 + 0 \times 1$
در نتیجه ضرب داخلی این دو بردار صفر است. لذا این دو بردار متعامد یا عمود بر هم هستند.
مثال ۲. برای اینکه دو بردار $(x^2 , -2 , 0) $ و $ (1 , x , 5)$ متعامد باشند. $x$ چه مقادیری را میتواند شامل شود؟
چون دو بردار متعامد هستند، داریم:
$(x^2 , -2 , 0) . (1 , x , 5) = x^2 -2x + 0 \times 5 = 0 \rightarrow x(x-2) = 0 \Rightarrow \begin{cases}x = 0\\ x = -2\end{cases}$
به ازای هر دو مقدار این دو بردار متعامد خواهند شد.
تمرین ۱. در چه شرایطی برای $x$ دو بردار $( x,1, 5x+1) , (2x , 0 , \frac{1}{5})$ متعامد هستند.
تمرین ۲. در چه شرایطی دو بردار $ (x^2 , 1, ,1, 0) $ و $ (x , 2x , 5, 0) $ متعامد خواهند شد.
- بازدید: 25414