خانه

تعریف ماتریس پوچ توان: فرض کنید ‎A‌‏ یک ماتریس ‌‎$n\times n ‌‌‌‎$‌‎ ‏باشد. ماتریس ‎A‌‏ را پوچ توان گویند، هرگاه عبارت زیر برقرار باشد:

$\exists k\in \mathbb{N}, A^k=0 , A^{k-1} \neq 0$

عبارت ریاضی بالا بیان می‌کند که k کوچکترین عدد طبیعی است که به ازای آن ماتریس A به توان آن عدد مساوی ماتریس صفر خواهد شد. در اینصورت ماتریس A را پوچ توان از مرتبه k گویند.

تذکر ۱. دقت کنید در صورتی که ماتریس ‎A‌‏ پوچ توان باشد، همواره اندیس ماتریس پوچ توان کمتر از تعداد سطرها یا ستون‌های ماتریس خواهد بود. یعنی برای ماتریس $n\times n$ که از مرتبه k پوچ توان است، داریم: ‎$‎ k‎ ‎\leq n ‌‌‎$‌‌‌‏.

مثال ۱. آیا ماتریس‌های زیر ماتریسی پوچ توان است؟

۱. $A=\begin{bmatrix}0 & 2 \\ 0 & 0 \end{bmatrix}$

با توحه به تعریف ماتریس پوچ توان، کافی است که ماتریس A را در خودش آنقدر ضرب کنیم که برای اولین بار، نتیجه این حاصلضرب‌ها صفر شود. برای این منظور به صورت زیر عمل می‌کنیم:

$A*A= \begin{bmatrix} 0 &2\\ 0&0 \end{bmatrix} \begin{bmatrix}0&2 \\0 & 0 \end{bmatrix}= \begin{bmatrix}0&0\\0&0\end{bmatrix}$

در نتیجه این ماتریس، ماتریس پوچ توان از مرتبه ۲ خواهد شد.

۲. $A=\begin{bmatrix} 0 & 0&2\\0&0&3\\0&0&0\\ \end{bmatrix}$

برای اینکه نشان دهیم این ماتریس، ماتریسی پوچ توان است یا خیر. کافی است به گونه‌ای که برای ماتریس بالا اقدام نمودیم عمل کنیم. حال ماتریس A را در خودش ضرب کنید:

$A*A=\begin{bmatrix} 0&0&3\\ 0&0&2\\ 0&0&0 \\ \end{bmatrix} \begin{bmatrix}0&0&3\\0&0&2\\0&0&0\\ \end{bmatrix} = \begin{bmatrix}0 &0&0 \\ 0&0&0 \\0&0&0\\ \end{bmatrix}$

در نتیجه این ماتریس هم پوچ توان از مرتبه 2 خواهد شد.

تمرین ۱. کدامیک از ماتریسهای زیر پوچ توان است. 

۱. $A=\begin{bmatrix}5&-3&2\\15&-9&6\\10&-6&4\\ \end{bmatrix}$

۲. $A=\begin{bmatrix}0&-3&2\\0&0&6\\0&0&4\\ \end{bmatrix}$

۳. $A=\begin{bmatrix}0&0&0&0\\1&0&0&0\\5&3&0&0\\8&6&5&0\\ \end{bmatrix}$

ماتریس شبه قطری: ماتریس $A$ به شکل زیر را در نظر بگیرید:

$A= \begin{bmatrix}A_1 & 0 & . & .& .& & 0 \\0 & A_2 & . & .& .& & 0\\ . & . & . & & & & . \\ . & . & & .& & & . \\ . & . & & & .& & . \\0 & 0 & . & .& .& & A_n \end{bmatrix}$

که در آن $A_1 , ... , A_n$ ماتریسهایی از مرتبه $m_i \times k_i$ برای $1\leq i\leq n$ باشند. در اینصورت ماتریس $A$ را یک ماتریس شبه قطری گویند. ماتریس شبه قطری $A$ را با نماد $A = diag (A_1 , ... , A_n)$ نمایش می‌دهند.

اگر ماتریس بلوکی را بخاطر بیاورید، ماتریس شبه قطری را می‌توانیم یک ماتریس بلوکی در نظر بگیریم که درایه های بلوک های غیر واقع بر قطر اصلی، همگی صفر باشند. 

جمع و ضرب روی ماتریس های شبه قطری: جمع و ضرب بر روی ماتریس‌های شبه قطری را به گونه زیر تعریف می‌کنیم:

فرض کنید که $A = diag (A_1 , ... , A_n)$ و $B = diag (B_1 , ... , B_n)$ ماتریس‌هایی شبه قطری باشند. جمع و ضرب بر روی این ماتریسهای شبه قطری زمانی قابل بیان است که ماتریس‌های $A_1 , ... , A_n , B_1 , ... , B_n $، به گونه‌ای باشند، که بتوان جمع و ضرب ماتریسی را برای این دو ماتریس شبه قطری بیان نمود. لذا برای جمع ماتریس‌های شبه قطری داریم:

$A+B = \begin{bmatrix}A_1 & 0 & . & .& .& & 0 \\0 & A_2 & . & .& .& & 0\\ . & . & . & & & & . \\ . & . & & .& & & . \\ . & . & & & .& & . \\0 & 0 & . & .& .& & A_n \end{bmatrix} + \begin{bmatrix}B_1 & 0 & . & .& .& & 0 \\0 & B_2 & . & .& .& & 0\\ . & . & . & & & & . \\ . & . & & .& & & . \\ . & . & & & .& & . \\0 & 0 & . & .& .& & B_n \end{bmatrix}= \begin{bmatrix}A_1+B_1 & 0 & . & .& .& & 0 \\0 & A_2+B_2 & . & .& .& & 0\\ . & . & . & & & & . \\ . & . & & .& & & . \\ . & . & & & .& & . \\0 & 0 & . & .& .& & A_n+B_n \end{bmatrix}$

و همچنین برای ضرب ماتریس‌های شبه قطری داریم:

$A.B = \begin{bmatrix}A_1 & 0 & . & .& .& & 0 \\0 & A_2 & . & .& .& & 0\\ . & . & . & & & & . \\ . & . & & .& & & . \\ . & . & & & .& & . \\0 & 0 & . & .& .& & A_n \end{bmatrix} . \begin{bmatrix}B_1 & 0 & . & .& .& & 0 \\0 & B_2 & . & .& .& & 0\\ . & . & . & & & & . \\ . & . & & .& & & . \\ . & . & & & .& & . \\0 & 0 & . & .& .& & B_n \end{bmatrix}= \begin{bmatrix}A_1.B_1 & 0 & . & .& .& & 0 \\0 & A_2.B_2 & . & .& .& & 0\\ . & . & . & & & & . \\ . & . & & .& & & . \\ . & . & & & .& & . \\0 & 0 & . & .& .& & A_n.B_n \end{bmatrix}$

مثال ۱. فرض کنید که A و B دو ماتریس شبه قطری به شکل زیر باشند. ضرب و جمع این دو  ماتریس را بدست آورید.

$ A = \begin{bmatrix}1 & 1 & & 0 & 0\\ 2 & 2 & & 0 & 0 \\ 0 & 0 & & 5 & 7& \\ 0 & 0 & & 8 & 9\end{bmatrix} , B = \begin{bmatrix}1 & 0 & & 0 & 0\\ 0 & 1 & & 0 & 0 \\ 0 & 0 & & 5 & 0& \\ 0 & 0 & & 0 & 5\end{bmatrix}$

$ A+B = \begin{bmatrix}2 & 1 & & 0 & 0\\ 2 & 3 & & 0 & 0 \\ 0 & 0 & & 10 & 7& \\ 0 & 0 & & 8 & 14\end{bmatrix} , A.B = \begin{bmatrix}1 & 1 & & 0 & 0\\ 2 & 2 & & 0 & 0 \\ 0 & 0 & & 25 & 35& \\ 0 & 0 & & 40 & 45\end{bmatrix} $

تمرین ۱.  ضرب و جمع ماتریس‌های شبه قطری زیر را محاسبه کنید.

$ A = \begin{bmatrix}5 & 7 & 10 & & 0 & 0 & 0\\ 8 & 9 & 11 & & 0 & 0 & 0 \\ 0 & 0 & 0 & & 5 & 7 & 6 \\ 0 & 0 & 0 & & 9 & 10 & 11\end{bmatrix} $

$ B = \begin{bmatrix}1 & 1 & 0 & & 0 & 0 & 0\\ 0 & 1 & 0 & & 0 & 0 & 0 \\ 0 & 0 & 0 & & 5 & 8 & 9 \\ 0 & 0 & 0 & & 0 & 1 & 1\end{bmatrix} $

ماتریس پائین مثلثی: فرض کنید که $A$ یک ماتریس مربعی از مرتبه $n \times n$ باشد. ماتریس $A$ را یک ماتریس پایین مثلثی گویند، هرگاه تمام درایه‌های بالای قطر اصلی آن صفر باشد. این موضوع را برحسب درایه‌های ماتریس $A = [a_{ij}]$ اینگونه بیان می‌کنیم:

$ \forall 1 \leq i , j \leq n ,             i \leq j \rightarrow a_{ij} = 0 $

تعریف ریاضی بالا بیان می‌کند، در یک ماتریس پایین مثلثی هر درایه‌ای که بر روی ستون با اندیس بالاتری نسبت به سطر واقع شده است، حتما صفر است.

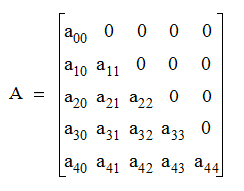
مثال ۱. فرض کنید ماتریس $A$ یک ماتریس پایین مثلثی باشد، که به گونه زیر تعریف شده است. در اینصورت مقادیر $xz+ y$ را بدست آورید.

$ A = \begin{bmatrix}0 & y & x \\5 & 0 & z \\ 3 & 1 & 0 \end{bmatrix} $

چون ماتریس $A$ یک ماتریس پایین مثلثی است، پس تمام درایه‌های بالای قطر اصلی آن صفر می‌باشد. لذا داریم $  0 =y = x = z$ در نتیجه $ xz+y = 0 $ خواهد بود.

تمرین ۱. کدام یک از ماتریسهای زیر، ماتریس بالا مثلثی و کدام یک ماتریس پایین مثلثی است.

۱. $ A = \begin{bmatrix}0 & 0 & 0 \\1 & 0 & 0 \\ 5 & 2 & 0 \end{bmatrix} $

۲. $ B = \begin{bmatrix}1 & 1 & 7 \\0 & 5 & 2 \\ 0 & 0 & 3 \end{bmatrix} $

۳. $ C = \begin{bmatrix}1 & 7 & 2 \\5 & 3 & 0 \\ 0 & 0 & 0 \end{bmatrix} $