خانه

تعریف ترانهاده یک ماتریس: ماتریسی که از جابه‌جایی جای عناصر سطر و ستون یک ماتریس حاصل می‌شود را ترانهادهٔ آن ماتریس می‌گویند. یا به عبارت دیگر، فرض کنید $A=[a_{ij}]‎$ یک‎ ماتریس ‏از مرتبه ‎$‎m‎\times n ‌‌‌‎$‌‎ باشد‏، ماتریس ‏از مرتبه ‎$‎ n‎\times ‎m‎$‌‌‏ که به وسیله تعویض سطرهای ماتریس A‌‏ ‌‎با‎ ستون‌های آن به دست می‌آید را ترانهاده ماتریس A‌‌‎ می‌گویند. ترانهاده ماتریس A را با نمادهای ‎$‌‎ ‎A‎^{T} ‌‎$‌‎ یا ‎$ ‎A‎^{‎t‎} $‌‏ نشان می‌دهیم. بصورت نمادهای ریاضی می‌توان ترانهاده یک ماتریس را به گونه زیر بیان نمود:

‎$ ‎A = [a‎_{ij}]‎_{‎m ‎\times ‎n‎}‎ ‌‎\rightarrow‎ A^T = [a‎_{ji}]‎_{‎m ‎\times ‎n‎} $‌‎

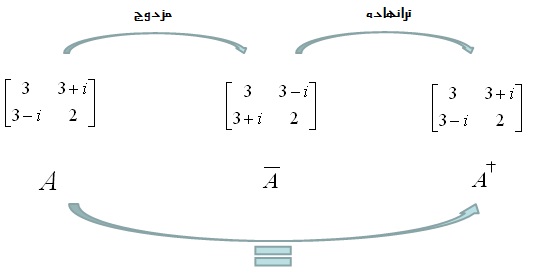
ماتریس‎ هرمیتی: ماتریس مربعی $A=[a_{ij}]_{n\times n}‎$ را در نظر بگیرید. هرگاه ترانهاده مزدوج مختلط آن با خود ماتریس برابر شود، آن ماتریس را یک ماتریس هرمیتی گویند. به عبارت دیگر، رابطه زیر بین درایه‌های ماتریس A و ماتریس هرمیتی A برقرار است: 

‎$‌‎ ‌‎\overline{A^{t}} =‎ A ‌‌‌‎$‌‌  ‏ یا ‎$‌‎ ‎a_{ij} =‎ ‌‎\overline{a_{ij}} ‌‎$‎

‏نکته ۱. با توجه به این موضوع که در ماتریس هرمیتی، درایه‌های ماتریس به صورت ‎$‎a_{ij} =‎ ‌‎\overline{a_{ij}} $‎ است، لذا عناصر واقع بر روی قطر اصلی ماتریس، نیز باید دارای این ویژگی باشد، یعنی‏ به ازای هر i خواهیم داشت:

‎$ ‎a_{ii}‎ =‎ ‌‎\overline{a_{ii}} $‎

با توجه به تعریف ماتریس هرمیتی که مزدوج مختلط آن باید با خود ماتریس برابر باشد، و همچنین این موضوع که هر عدد با مزدوج مختلط خود زمانی برابر خواهد بود که آن عدد حقیقی باشد. لذا عناصر بر روی قطر اصلی ماتریس هرمیتی همیشه اعداد حقیقی خواهند بود.

نکته ۲.  ماتریسهای متقارن حقیقی، ماتریس‌های هرمیتی می‌باشند، زیرا عبارت زیر را برای ماتریس‌های متقارن حقیقی داریم:

‎$ ‎a_{ij} =‎ ‌‎\overline{a_{ij}} ‎\Longrightarrow ‎a_{ij} = ‎a_{ji}‎ $‌‏

مثال ۱. با ذکر علت بیان کنید کدامیک از  ماتریسهای زیر، ماتریس هرمیتی است.

۱. $A = \begin{bmatrix} 0 &i & 0 \\ -i & 1 & 2 \\ 0 & 2 & i\end{bmatrix}$

با توجه به نکته ۱، زمانیکه یک ماتریس مربعی، ماتریس هرمیتی باشد، درایه‌های واقع بر روی قطر اصلی آن حتما حقیقی خواهند بود. پس با توجه به این موضوع، ماتریس A، ماتریس هرمیتی نخواهد بود، زیرا درایه آخر از قطر اصلی عددی موهومی است.

۲.  $B = \begin{bmatrix}1& i& 1-i\\ -i& 1& 0 \\ 1+i & 0 & 1 \end{bmatrix}$

 ماتریس B یک ماتریس هرمیتی است، برای بررسی این موضوع کافی است ثابت کنیم که ترانهاده مزدوج این ماتریس با خود ماتریس برابر خواهد شد. ابتدا با مزدوج نمودن تک تک درایه‌های ماتریس B، مزدوج این ماتریس را به گونه زیر به دست می‌آوریم:

$‌‎\overline{B} = \begin{bmatrix}1& -i& 1+i\\ i& 1& 0 \\ 1-i & 0 & 1 \end{bmatrix}$

و در نهایت با ترانهاده گرفتن از ماتریس مزدوج، ماتریس نهایی را به گونه زیر حاصل می‌کنیم:

$\overline{B}^T= \begin{bmatrix}1& i& 1-i\\ -i& 1& 0 \\ 1+i & 0 & 1 \end{bmatrix}$

حال اگر به ترانهاده مزدوج ماتریس B و خود ماتریس B دقت کنید متوجه خواهید شد که این دو ماتریس یکسان می‌باشند.

در ادمه این مطلب سعی نموده‌ایم که ویژگی‌های مهم ماتریس هرمیتی را همراه با مثالی برای تک تک آنها بیان کنیم.   

 ویژگی ۱. هر ماتریس هرمیتی‏، یک ماتریس نرمال می‌باشد. زیرا از تعریف ماتریس هرمیتی داريم‎$ ‌‌‎\overline{A ^ {t}}‎ =‎ A ‌‌‌‎$‌‌‏. با ضرب كردن دو طرف اين عبارت در ماتریس A خواهيم داشت:

$ ‌‌‎A\overline{A ^ {t}}‎ =‎ AA=\overline{A ^ {t}}A ‌‌‌‎$‌‌

 از دو طرف عبارت بالا خواهیم داشت:

‎$‌‎ ‎A\overline{A^t}= ‌‌‌‎\overline{A^t}A ‌‎$ ‌‏

که نشان می‌دهد A یک ماتریس نرمال است.

مثال ۲.  آیا  ماتریس زیر یک ماتریس نرمال است.

$A=  \begin{bmatrix} 1& 1-i\\ 1+i& 0 \end{bmatrix}$

با توجه به ویژگی بالا، و این موضوع که ماتریس A، یک ماتریس هرمیتی است، لذا A یک ماتریس نرمال هم خواهد بود. 

ویژگی ۲. مقادیر ویژه‌ ماتریس‌های هرمیتی‏، عددهای حقیقی می‌باشند.

برای نشان دادن این موضوع کافی است به گونه زیر عمل کنید، فرض کنید که $\lambda$ یک مقدار ویژه دلخواه از ماتریس هرمیتی A باشد. در اینصورت داریم:

$Ax=\lambda x$ 

اکنون دو طرف تساوی بالا را در $\overline{x}^T$ ضرب می‌کنیم، لذا داریم:

$\overline{x}^T(Ax)=\overline{x}^T(\lambda x)=\lambda\overline{x}^T x=\lambda \| x \|$        (*)

حال با توجه به این موضوع که x , Ax دو بردار می‌باشند، لذا با توجه به ضرب داخلی بردارها داریم:

$\overline{x}^T(Ax)=(Ax)^T \overline{x}$

با توجه به ویژگی ترانهاده هم رابطه عبارت زیر حاصل خواهد شد:

 $\overline{x}^T(Ax)=(Ax)^T \overline{x}=x^T A \overline{x}$                                                (**)

در نهایت با مزدوج گرفتن از دو طرف تساوی عبارت (*) داریم:

$x^T\overline{A}\overline{x}=\overline{\lambda} \| x \|$                                                      (***)

حال با توجه به (*)،(**) و (***) خواهیم داشت:

$\overline{\lambda} \| x \| =\lambda \| x\|⇒ \overline{\lambda}=\lambda$

از عبارت حاصل شده $\overline{\lambda}=\lambda$ می‏‌توان نتیجه گرفت که مقادیر ویژه‌های ماتریس هرمیتی حتما حقیقی است زیرا اعدادی که مزدوج آنها با خود آن عدد یکی باشد حتما اعداد حقیقی خواهند بود.

۳. بردارهای ویژه ماتریس هرمیتی‏، متعامد هستند.

برای نشان دادن این موضوع کافی است دو مقدار ویژه متمایز $\lambda_1 , \lambda_2$ را با بردارهای ویژه متناظر به ترتیب $x_1 , x_2$ در نظر بگیریم. از آنجا که این مقادیر ویژه حقیقی هستند، داریم: 

$\lambda_1(x_1 , x_2)=(\lambda_1 x_1 , x_2)=(Ax_1 , x_2)=(x_1 , Ax_2)=(x_1 , \lambda_2 x_2)=\lambda_2 (x_1 , x_2)$

از متمايز بودن دو مقدار ويژه $\lambda_1 , \lambda_2$ داریم، زمانی تساوی دو طرف عبارت بالا برقرار خواهند شد که عبارت $(x_1 , x_2)$ مساوی صفر شود و این موضوع با توجه به مفهوم ضرب داخلی فضای برداری به این معنی است که این دو بردار متعامد خواهند بود.

مثال ۱. مقادیر و بردارهای ویژه ماتریس هرمیتی زیر را مورد محاسبه قرار دهید.

‎$ A = \begin{bmatrix}1 & 1-‎i‎ \\ 1 + i & 2 \end{bmatrix} $‌‌‎

برای محاسبه مقدارهای ویژه باید عبارت ‌‎$ ‎det ‎(A -‎ ‌‎\lambda ‎I) =‎ 0 ‌‌‌‎$‌‎ ‏را محاسبه کنیم. لذا داريم:

‎$ A -‎ ‌‎\lambda I‎ =‎ \begin{bmatrix}1 & 1-‎i‎ \\ 1 + i & 2 \end{bmatrix} -‎ ‌‎\begin{bmatrix}‎ ‌‎\lambda &0 \\ 0& ‎ ‌‎\lambda \end{bmatrix} =‎ \begin{bmatrix}1- ‌‎\lambda & 1-‎i‎ \\ 1 + i & 2 - ‌‎\lambda \end{bmatrix}‌‎ $‌‌‎

اکنون دترمینان ماتریس حاصل را بدست می آوریم:

‎$‌‎ ‎det\begin{bmatrix}1- ‌‎\lambda & 1-‎i‎ \\ 1 + i & 2 - ‌‎\lambda \end{bmatrix} =‎ (1 - ‌‎\lambda) ‎(2 - ‌‎\lambda) -‎ ‎(1 -‎ ‎i) (‎ ‎1+i) =‎ ‎2 - ‌‎\lambda -‎ ‎2‌‎\lambda +‌‌‎\lambda^2 ‎-1 -‎ i‎ ‎+i ‎-1 = ‌‌‌‎\lambda^2 -3\lambda‌‎ ‎\Longrightarrow ‌‎\lambda =‎ 0‎ , ‌‌‌‎\lambda =‎ 3 ‌‌‌‎$‌‌‏ .

حال برای بدست آوردن بردارهای ویژه اینگونه عمل می‌کنیم که ‎$‌‎ ‎Av = ‌‌‌‎\lambda‎ v ‎$‎. ابتدا بردار ویژه $v=(v_1 , v_2)$ متناظر با مقدار ویژه $\lambda =0$  را به دست می‌آوریم:

$Av=0\times v=0 ⇒ \begin{bmatrix}1 & 1-‎i‎ \\ 1 + i & 2 \end{bmatrix} (v_1 , v_2)^T=0 ⇒ \begin{bmatrix}v_1 + v_2(1-‎i)‎ \\ v_1 (1 + i) + 2v_2 \end{bmatrix} $ 

در نتيجه از مولفه اول بردار حاصل شده يعنی $v_1 = -(1-i)v_2$ داریم که بردار ویژه متناظر با مقدار ویژه صفر به صورت $v=(-(1-i) , 1)$ خواهد شد. با روشی مشابه بردار ویژه متناظر با مقدار ویژه ۳ را محاسبه کنید. 

تمرین ۱. مقدار ویژه و بردارهای ویژه ماتریس هرمیتی زیر را بدست آورید.

‎$ A = \begin{bmatrix}1 & -‎i‎ & 1 \\ i & 0 & 3 \\ 1 & 3 & 2 \end{bmatrix} $‎

تعریف ضرب ماتریس دو ماتریس: فرض کنیم ‎$‎ A‎ = ‌‎[a_{ij}]_{m ‌‎\times ‎n} $‌‌‎ و ‎$ B‎ =‎ [‎‎b_{ij}]_{n ‌‌‌‎\times k} ‌‎$‎ ‏دو ماتريس ‏باشند. حاصلضرب ماتریس A در ماتریس B برابر با ماتریس ‎$ C‎ =‎ [‎ ‎c_{ij} ‎] ‌‌‌‎$‌‎ از مرتبه $m ‌‎\times k$ است که آن را با نماد ‎AB‌‏ نشان می‌دهیم و به صورت زیر تعریف می‌کنیم:

 ‌‎$ C_{ij} =‎ ‌‎\sum_{r=1}^‎{n} {‎a_{ir}b_{rj}} ‎ ‎\forall 1‎ ‌‎\leq i ‌‌‌‎\leq m‎ ,‎ 1‎ ‎\leq j‎ ‎\leq n ‌‌‌‎$‌‎

تعریف ریاضی بالا بیان می‌کند، برای به دست آوردن درایه ijام ماتريس C کافی است، سطر iام ماتريس A را در ستون jام ماتريس B ضرب کنید. شکل زیر کمک شایانی به درک هرچه بهتر این موضوع خواهد نمود. 

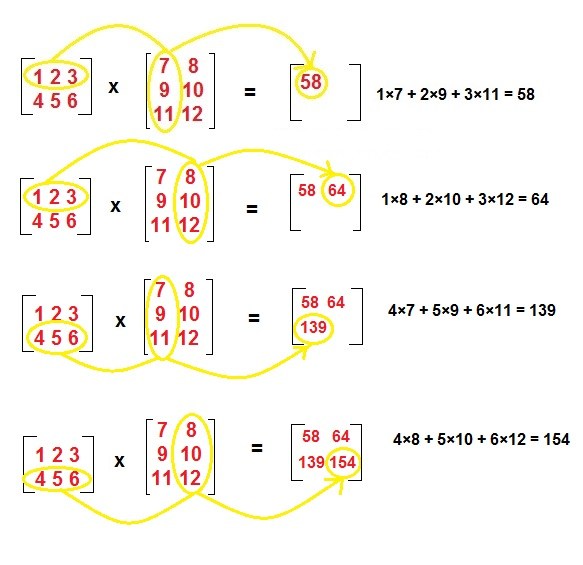
مثال ۱. ضرب ماتریس زیر را به دست آورید.

۱. $ A = \begin{bmatrix}1 & -‎i‎ & 1 \\ i & 0 & 3 \\ 1 & 3 & 2 \end{bmatrix} $‎ , $ B = \begin{bmatrix}0 & -‎i‎ & 2 \\ 5 & 0 & 3i \\ i+1 & 3 & 2 \end{bmatrix} $‎

با توجه به تعریف بالا برای ضرب ماتریس‌ها داریم:

$ A.B= \begin{bmatrix}1 & -‎i‎ & 1 \\ i & 0 & 3 \\ 1 & 3 & 2 \end{bmatrix}\begin{bmatrix}0 & -‎i‎ & 2 \\ 5 & 0 & 3i \\ i+1 & 3 & 2 \end{bmatrix} \\ = \begin{bmatrix}1\times0-i\times 5 + 1\times (i+1) &1\times(-‎i)+0\times (-i)+1\times 3‎ & 1\times 2 +(-i)\times 3i + 1\times 2\\ i\times 0+0\times 5+3\times (i+1) & i\times (-i)+0+3\times 3 & i\times 2+0\times 3i+3\times 2 \\ 1\times 0+3\times 5+2\times (i+1) & 1\times (-i)+3\times 0+2\times 3 & 1\times 2+3\times 3i+2\times 2 \end{bmatrix} $‎

$= \begin{bmatrix}4i+1 & -‎i‎+3 & 4 \\ 3i+3 & 10 & 6+2i \\ 2i+17 & 6-i& 6+9i\end{bmatrix}$

نکته ۱. زمانی می‌توانید ماتریس A‌‌‌‏ را در ماتریس B‌‌‎ ضرب کنید که تعداد ستون‌های ماتریس A‌‌‎ با تعداد سطرهای ماتریس B‌‌‎ برابر باشد.

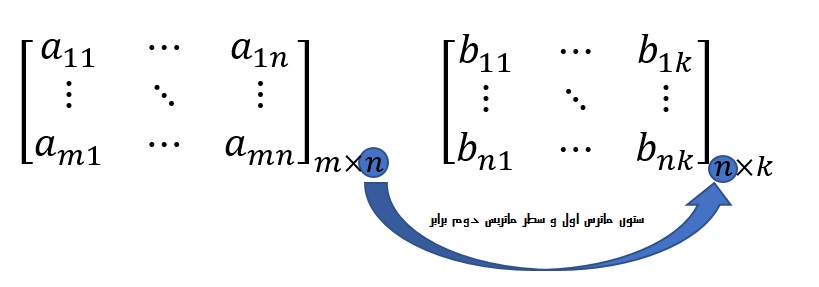
از شکل بالا متوجه خواهید شد که دو ماتریس زیر قابل ضرب شدن نیستند، زیرا با توجه به تعریف ضرب ماتریسی حتما باید تعداد ستون‌های ماتریس اول با تعداد سطرهای ماتریس دوم برابر باشند.  

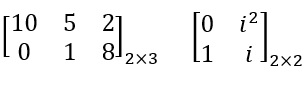
مثال ۲. حاصلضرب ماتریس‌های زیر را بدست آورید.

۱. ‎$ A = \begin{bmatrix}1 & 5 & 7 \\ 8 & 9 & 2 \end{bmatrix} , ‎B‎ = \begin{bmatrix}1 & 2 \\ 0 & 1 \\ 0 & 1 \end{bmatrix}‎ $ ‌

    ⇒ $AB= \begin{bmatrix}1 & 5 & 7 \\ 8 & 9 & 2 \end{bmatrix}\begin{bmatrix}1 & 2 \\ 0 & 1 \\ 0 & 1 \end{bmatrix}‎$ = $\begin{bmatrix}1 & 2+5+7 \\ 8 & 16+9+2 \end{bmatrix}$  ⇒  $\begin{bmatrix}1 & 14 \\ 8 & 27 \end{bmatrix}$

۲. ‎$ A = \begin{bmatrix} 5 & 7 \end{bmatrix} , ‎B‎ = \begin{bmatrix} 8 & 9 \end{bmatrix} $‎

با توجه به نکته ۱، باید تعداد ستون‌های ماتریس A با تعداد سطرهای ماتریس B یکسان باشد. اما همانطور که مشاهده می‌کنید تعداد ستون‌های ماتریس A برابر با ۲ و تعداد سطرهای ماتریس B برابر با ۱ می‌باشد. در نتیجه با توجه به نکته ۱، دو ماتریس فوق قابل ضرب شدن نمی‌باشند. 

۳. ‎$ A = \begin{bmatrix} 5 & 4 ‎\\ 2‎ &‎ ‎2‎ \end{bmatrix} , ‎B‎ = \begin{bmatrix} 1 & 2 ‎\\ 0‎ & ‎1‎ \end{bmatrix} $‌‎

   ⇒ $ AB = \begin{bmatrix} 5 & 4 \\ 2 & 2 \end{bmatrix} \begin{bmatrix} 1 & 2 \\ 0 & 1 \end{bmatrix} = \begin{bmatrix} 5 & 14\\ 2 & 6 \end{bmatrix}$

تعریف توان یک ماتریس: ‏فرض کنید که ‌‏A‌‌‌‎ یک ماتریس‎$‎ n ‌‌‌‎\times n ‌‌‌‎$‌‌‏ باشد. در این صورت توان ‎k‌‏ام ماتریس A‎‎ به این معنی است که ‎ k‌‏بار‎ ماتریس A‌‌‎ را در خودش ضرب نمایید.

‎$‎ A‎ ‎\times ‎... ‌‎\times A‎ =‎ ‎A^{k} ‌‎$ ‌‎

مثال ۳. توان سوم ماتریس مربعی زیر را به دست آورید. 

$A= \begin{bmatrix} 1 & 2 \\ 2‎ &‎ ‎2‎ \end{bmatrix}$

$A^3= A.A.A=\begin{bmatrix} 1 & 2 \\ 2‎ &‎ ‎2‎ \end{bmatrix}\begin{bmatrix} 1 & 2 \\ 2‎ &‎ ‎2‎ \end{bmatrix}\begin{bmatrix} 1 & 2 \\ 2‎ &‎ ‎2‎ \end{bmatrix} = \begin{bmatrix} 1+4 & 2+4 \\ 2+4‎ &‎ ‎4+4‎ \end{bmatrix}\begin{bmatrix} 1 & 2 \\ 2‎ &‎ ‎2‎ \end{bmatrix}$

⇒ = $\begin{bmatrix} 5 & 6 \\ 6 &‎ ‎8‎ \end{bmatrix}\begin{bmatrix} 1 & 2 \\ 2‎ &‎ ‎2‎ \end{bmatrix}= \begin{bmatrix} 17 & 22 \\ 2‎2 &‎ ‎28‎ \end{bmatrix}$

‏نکته ۲. دقت کنید که دو ماتریس مربعی هم مرتبه ‎A‌‏ و ‎B‌‌‏، نسبت به ضرب ماتریسی خاصیت جابه‌جایی ندارند.

مثال ۴. بررسی کنید که رابطه AB=BA نسبت به ضرب ماتریسی برقرار نمی‌باشد؟

برای این منظور کافی است که دو ماتریس مثال بزنید که این موضوع را نقض کند. دو ماتریس زیر را در نظر بگیرید:

$A=\begin{bmatrix} 0 & 1 \\ 1 &‎ ‎1‎ \end{bmatrix} , B=\begin{bmatrix} 1 & 1 \\ 0 & 1 \end{bmatrix}$

⇒ $AB= \begin{bmatrix} 0 & 1 \\ 1 &‎ ‎1‎ \end{bmatrix} \begin{bmatrix} 1 & 1 \\ 0 & 1 \end{bmatrix} = \begin{bmatrix}0 & 1 \\ 1 & 2 \end{bmatrix}$

⇒ $BA= \begin{bmatrix} 1 & 1 \\ 0 & 1 \end{bmatrix} \begin{bmatrix} 0 & 1 \\ 1 & 1 \end{bmatrix} =\begin{bmatrix} 1 & 2 \\ 1& 1\end{bmatrix}$

در نتیجه ضرب ماتریسی دارای خاصیت جابه‌جایی نمی‌باشد.

تمرین. حاصلضرب ماتریس‌های زیر را در صورت امکان به دست آورید.

1. $ A=\begin{bmatrix} 5 & 1 & 0\\ 2 & 1 & 3 \end{bmatrix} , B= \begin{bmatrix} 8 & 1 \\ 1& 1\end{bmatrix}$

۲. $ A=\begin{bmatrix} a & b \\ 2 & c \end{bmatrix} , B= \begin{bmatrix} 8 & 0 \\ 0 & 1 \\3 & q \end{bmatrix}$