خانه

مزدوج ماتریس: فرض کنید که $A$ یک ماتریس از مرتبه $ m \times n$ باشد. ماتریسی که از مزدوج کردن تک تک درایه‌های ماتریس $A$ حاصل می‌شود، را مزدوج ماتریس $A$ گویند. به عبارت دیگر فرض کنید $A = [a_{ij}]$ باشد. در اینصورت مزدوج ماتریس $A$ را با نماد $\overline{A} = [b_{ij}]_{m \times n}$ نمایش می‌دهند، که رابطه زیر بین درایه‌های $A$ و  $\overline{A}$ برقرار می‌باشد:

$b_{ij} = \overline{a_{ij}}$

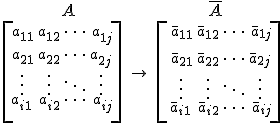
مثال ۱. مزدوج ماتریس‌های زیر را محاسبه کنید.

۱. $A = \begin{bmatrix} 1 & 5i & i \\ 2 & 0 & i+1 \end{bmatrix} \Longrightarrow \overline{A} = \begin{bmatrix} 1 & -5i & -i \\ 2 & 0 & 1-i \end{bmatrix}$

۲. $B = \begin{bmatrix} 5i+3 & 2i+1 \\ 3i+7 & 5i \end{bmatrix} \Longrightarrow \overline{B} = \begin{bmatrix} 3-5i & 1-2i \\ 7-3i & -5i \end{bmatrix}$

تمرین ۱. مزدوج ماتریس‌های زیر را بدست آورید.

۱. $A = \begin{bmatrix} 1 & i & 2i+1 \\ \frac{5i+1}{2i} & 0 & \frac{2i+1}{3i} \end{bmatrix}$

۲. $B = \begin{bmatrix} 1+ \sqrt{2i} & 5 \\ 0 & (3i+5)(2i+1) \end{bmatrix}$

ویژگی‌های مزدوج ماتریس: برای ماتریس‌های مزدوج ویژگی‌های زیر را داریم:

ویژگی ۱. فرض کنید که $A$ یک ماتریس $m \times n$ باشد. در اینصورت داریم:

$\overline{\overline{A}} = A$

یعنی مزدوج، مزدوج یک ماتریس با خود ماتریس برابر است.

مثال ۱. فرض کنید که $A = \begin{bmatrix} i & 2i \\ 5i+1 & 3i \end{bmatrix}$ باشد. در اینصورت نشان دهید که $\overline{\overline{A}} = A$ خواهد بود.

$A = \begin{bmatrix} i & 2i \\ 5i+1 & 3i \end{bmatrix} \Longrightarrow \overline{A} = \begin{bmatrix} -i & -2i \\ 1-5i & -3i \end{bmatrix} \Longrightarrow \overline{ \overline{A}} = \begin{bmatrix} i & 2i \\ 5i+1 & 3i \end{bmatrix}$

که در اینصورت $\overline{\overline{A}} = A$ می‌باشد.

ویژگی ۲. فرض کنید که $A$ یک ماتریس $ m \times n$ و $k$ یک عدد مختلط باشد. در اینصورت داریم:

$\overline{kA} = \overline{k} . \overline{A}$

مثال ۲. فرض کنید که $A$ یک ماتریسی باشد که به صورت زیر تعریف شده است و $k =2i$ باشد. ویژگی ۲ را نشان دهید.

$A = \begin{bmatrix} 1 & 2i \\ -4i & 0 \end{bmatrix}$

⇒  $\overline{A} = \begin{bmatrix} 1 & -2i \\ 4i & 0 \end{bmatrix}$

⇒ $kA = \begin{bmatrix} 2i & -4 \\ 8 & 0 \end{bmatrix} \Longrightarrow \overline{kA} = \begin{bmatrix} -2i & -4 \\ 8 & 0 \end{bmatrix}$

⇒ $k=2i \rightarrow \overline{k} = -2i$

⇒ $\overline{kA} = \begin{bmatrix} -2i & -4 \\ 8 & 0 \end{bmatrix}$

⇒ $\overline{k} . \overline{A} = (-2i) . \begin{bmatrix} 1 & -2i \\ 4i & 0 \end{bmatrix} = \begin{bmatrix} -2i & -4 \\ 8 & 0 \end{bmatrix}$

در نتیجه $\overline{kA} = \overline{k} . \overline{A}$

ویژگی ۳. فرض کنید که $A$  و $B$ دو ماتریس $ m \times n$ باشند. در اینصورت داریم:

$\overline{A+B} = \overline{A} + \overline{B}$

تمرین ۱. فرض کنید که $A$ و $B$  ماتریسهایی به شکل زیر باشند. ویژگی ۳ را برای حالت‌های مختلف  $A$ و $B$ محاسبه کنید.

۱. $ A = \begin{bmatrix} 1 & \frac{2i+1}{1+i} \\ \frac{3i}{1+2i} & 0 \end{bmatrix} , B = \begin{bmatrix} 5i(5i+1) & 0 \\ 2(1+i) & 0 \end{bmatrix}$

۲. $ A = \begin{bmatrix} 0 & 1 & i+1 \\ 2i & 3i & 0 \\ 0 & 0 & 5 \end{bmatrix} , B = \begin{bmatrix} \frac{1+i}{2i} & 0 & \frac{1+5i}{2i} \\ 0 & 1 & 0 \\ 0 & 5i & 3i \end{bmatrix}$

ویژگی ۴. فرض کنید که $A$ یک ماتریس از مرتبه $ m \times n$ و $B$ یک ماتریس از مرتبه $ n \times k$ باشند. در اینصورت داریم:

$ \overline{AB} = \overline{A} \overline{B} $

تمرین ۲. فرض کنید که $A$ و $B$  ماتریسهایی به شکل زیر باشند. در اینصورت ویژگی‌ ۴ را برای آنها بررسی کنید.

$ A = \begin{bmatrix} i & 2i+5 \\ 3i\sqrt{2} & 7i \end{bmatrix} , B = \begin{bmatrix} (i+1)^2 & 3i \\ 2i & 5 \end{bmatrix}$

$ A = \begin{bmatrix} 0 & 1 & i+1 \\ 2 & i & i+1 \\ 2 & 3i & 3i(3i+1) \end{bmatrix} , B = \begin{bmatrix} 0 & 1 & 0 \\ 1 & 1 & 5i \\ 2i & 0 & 0 \end{bmatrix}$

ویژگی ۵. فرض کنید که $A$ یک  ماتریس $ m \times n$ باشد. در اینصورت داریم:

$\overline{A^t} = \overline{A}^t$

مثال ۳. فرض کنید که $A$ یک  ماتریس به شکل زیر باشد. ویژگی ۵ را بررسی کنید.

$A = \begin{bmatrix} 1 & 2i & 5 \\ 3i & 7i+1 & 5i \end{bmatrix} \Longrightarrow \overline{A} = \begin{bmatrix} 1 & -2i & 5 \\ -3i & 1-7i & -5i \end{bmatrix} \Longrightarrow \overline{A}^t = \begin{bmatrix} 1 & -3i \\ -2i & 1-7i \\ 5 & -5i \end{bmatrix}$

$ A^t = \begin{bmatrix} 1 & 3i \\ 2i & 1+7i \\ 5 & 5i \end{bmatrix} \Longrightarrow \overline {A^t} = \begin{bmatrix} 1 & -3i \\ -2i & 1-7i \\ 5 & -5i \end{bmatrix}$

در نتیجه $ \overline{A^t} = \overline{A}^t$ خواهد بود.

تمرین ۳. برای ماتریسهای زیر و اسکالر $ k = 2i-1$ تمام ویژگی های ۱ تا ۵ را بررسی کنید.

$ A = \begin{bmatrix} i & 5 & i+1 \\ 2 & 1 & 1 \\ 0 & 1 & 1 \end{bmatrix}$

$ B = \begin{bmatrix} i & 1 & 2 \\ 0 & 1 & 5i-1 \\ 2i & 0 & 1 \end{bmatrix}$

زیرماتریس: فرض کنید که $A$ یک ماتریس $m \times n$ باشد. در اینصورت یک زیرمجموعه از سطرها و یک زیرمجموعه از ستون‌های ماتریس $A$ با هم ماتریس جدیدی را ایجاد می‌کند، که آن را زیرماتریسی از ماتریس $A$ گویند. به عبارت دیگر این موضوع را می‌توان با استفاده از نمادهای ریاضی به گونه زیر بیان نمود:

فرض کنید که $A$ یک ماتریس $m \times n$ باشد. یک زیر ماتریس از ماتریس $A$ به صورت زیر مشخص می‌شود:

۱. $\{ a_1 , ... , a_r \}$، مجموعه $r$ اندیس‌ انتخاب شده از کل $m$ سطر ماتریس A می‌باشد.

۲. $\{ b_1 , ... , b_s \}$، مجموعه $s$ ستون انتخاب شده از کل $n$ ستون ماتریس A می‌باشد.

در نتیجه زیرماتریس تشکیل شده از سطرها با اندیس‌های $\{ a_1 , ... , a_r \}$ و از ستون‌ها با اندیس‌های $\{ b_1 , ... , b_s \}$ به صورت زیر مشخص می‌شوند:

$A = [a_1 , a_2 , ... , b_a , b_2 , ... , b_s] $

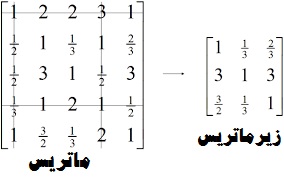
برای مثال، ماتریس زیر را در نظر بگیرید. برای تشکیل زیرماتریس، ابتدا سطرها و ستون‌های  ۲، ۳ و ۵ را انتخاب می‌کنیم و با استفاده از آنها زیرماتریس را به صورت زیر تشکیل می‌دهیم. به عبارت دیگر سطرها و ستون‌های اول و چهارم را از ماتریس اصلی حذف می‌کنیم ( روی آن خط خورده است)  

مثال ۱. سه زیرماتریس،  ماتریس زیر را مشخص کنید.

$A = \begin{bmatrix} 1 & 0 & 5 \\ 2 & 3 & 7 \\ 8 & 9 & 10 \end{bmatrix} $

⇒ $A_1 = \begin{bmatrix} 1 & 0 \\ 2 & 3 \end{bmatrix}$

⇒ $A_2 = \begin{bmatrix} 1 & 0 & 5 \\ 2 & 3 & 7 \end{bmatrix}$

⇒ $A_3 = \begin{bmatrix} 1 & 0 \\ 2 & 3 \\ 8 & 9 \end{bmatrix}$

نکته ۱. فرض کنید که $A$ یک ماتریس $ m \times n$ باشد. تعداد کل زیرماتریس‌های از مرتبه $k_1 \times k_2$ برابر است با

$\begin{pmatrix} m \\ k_1 \end{pmatrix} \begin{pmatrix} m \\ k_1 \end{pmatrix} = \frac{m! n!}{(m-k_1)! k_1!k_2!(n-k_2)!}$

و همچنین تعداد کل زیرماتریس‌های یک ماتریس از مرتبه $m \times n$ برابر است با

$\sum_{k_1=1}^m \sum_{k_2=1}^n \left(\begin{array}{c}m\\ k_1\end{array}\right)\left(\begin{array}{c}n\\ k_2\end{array}\right) = (2^m-1)(2^n-1)$

مثال ۲. فرض کنید که $A$ یک ماتریس $ 5 \times 4$ باشد . تعداد کل زیرماتریس‌های از مرتبه‌های $3 \times 3$ ،$ 1 \times 2 $ و $ 2 \times 3 $ را به دست آورید، و همچنین تعداد کل زیرماتریس‌های ماتریس $A$ را محاسبه کنید.

برای محاسبه تعداد زیرماتریس‌ها به گونه زیر عمل می‌کنیم:

$\left(\begin{array}{c}5\\ 2\end{array}\right)\left(\begin{array}{c}4\\ 3\end{array}\right) = \frac{5! 4!}{2! 3!(5-2)!(4-3)!} = \frac{5! 4!}{2! 3! 3! 1!}$

$\left(\begin{array}{c}5\\ 1\end{array}\right)\left(\begin{array}{c}4\\ 2\end{array}\right) = \frac{5! 4!}{1! 2!(5-1)!(4-2)!} = \frac{5! 4!}{2! 4! 2!}$

$\left(\begin{array}{c}5\\ 3\end{array}\right)\left(\begin{array}{c}4\\ 3\end{array}\right) = \frac{5! 4!}{3! 3!(5-3)!(4-3)!} = \frac{5! 4!}{3! 3! 2!}$

و تعداد کل زیرماتریس‌های این ماتریس عبارتند از:

$\sum_{k_1 =1}^5 \sum_{k_2 =1}^4\left(\begin{array}{c}5\\ k_1\end{array}\right)\left(\begin{array}{c}4\\ k_2\end{array}\right) = (2^5-1)(2^4-1) = 31 \times 15$

تمرین ۱. تعداد کل زیرماتریس‌های از مرتبه‌های $5 \times 6$، $8\times 2$ و $3\times 2$ از یک ماتریس از مرتبه $12\times 7$ را محاسبه کنید.