خانه
ماتریس بلوکی
ماتریس بلوکی: فرض کنید A یک ماتریس دلخواه باشد. هر گاه بین سطرها و ستونهای ماتریس A، خطوطی افقی و عمودی دلخواهی رسم کنیم و ماتریس A را تقسیم نماییم، در اینصورت ماتریس A را بلوکبندی کردهایم. دقت کنید که با تغییر جای این خطوط افقی و عمودی میتوانید بلوکبندیهای متفاوتی از این ماتریس را به دست آورید. برای مثال، شکل زیر یک بلوکبندی از ماتریس A را نمایش میدهد.
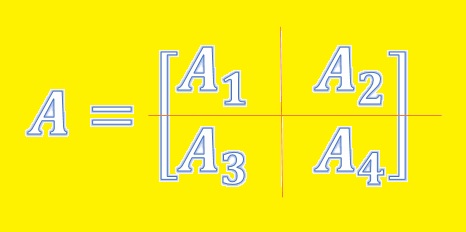
مثال ۱. سه بلوکبندی متفاوت از ماتریس A را به دست آورید.
$A=\begin{bmatrix} 1& 2 & 0\\ 0 & 5 & 7\\ 0 & 1 & 3 \end{bmatrix}$
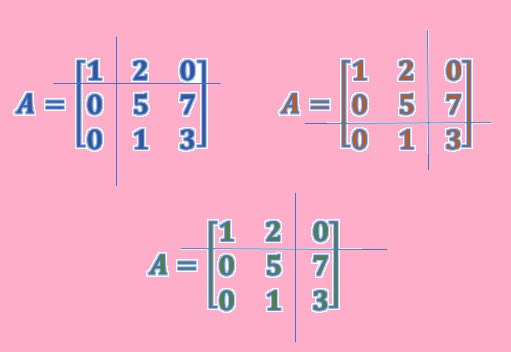
تمرین ۱. سه بلوکبندی متفاوت برای ماتریسهای زیر را محاسبه کنید.
۱. $A=\begin{bmatrix} 1& 2 & i &5\\ 4&1 & 5 & 7\\ 12& 0 & 1 & 3 \end{bmatrix}$
۲. $A=\begin{bmatrix} 0& 2 & 0\\ 0 & 5 & 9 \end{bmatrix}$
۳. $A=\begin{bmatrix} 10& 20 & 0\\ 0 & 15 & 0\\ 0 & 1 & 3 \end{bmatrix}$
قضیه ۱. فرض کنید که A و B دو ماتریس هم مرتبه باشند. برای این دو ماتریس، بلوکبندی را به گونه زیر انجام میدهیم که ضرب AB قابل تعریف باشد.
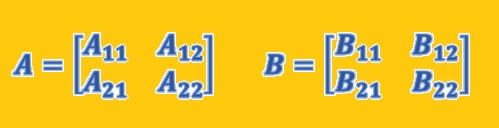
در اینصورت ماتریس AB را به صورت زیر خواهیم داشت:
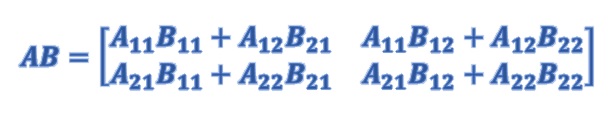
تمرین ۲. حاصلضرب ماتریسهای زیر را با دو تقسیم بلوکی محاسبه کنید.
$A=\begin{bmatrix}1&2&3&4\\5&6&7&8\\9&10&11&12\\13&14&15&16 \end{bmatrix}$
$B=\begin{bmatrix}0&1&0&4\\0&0&7&1\\0&0&1&2\\3&4&1&1 \end{bmatrix}$
- بازدید: 15039
ماتریس متقارن
تعریف ماتریس متقارن: فرض کنید که A یک ماتریس مربعی از مرتبه $ n $ باشد. ماتریس A را متقارن گویند، هرگاه با ترانهاده اش برابر باشد یعنی داشته باشیم:
$ A^{T} = T $
در واقع این عبارت بالا بیان میکند که در ماتریس متقارن A رابطه زیر بین داریههای ماتریس برقرار باشد.
$ \forall 1 \leq i , j \leq n ⇒ a_{ij} = a_{ji} $
به زبان ساده تر این که وقتی یک ماتریس متقارن است، درایههای آن نسبت به قطر اصلی متقارن میباشند و برعکس اگر درایه های ماتریسی نسبت به قطر اصلی متقارن باشند آن ماتریس را ماتریس متقارن گوییم.
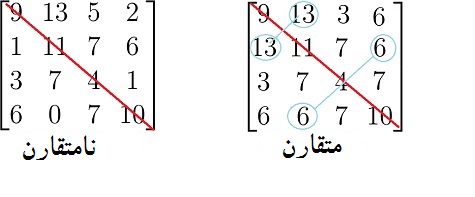
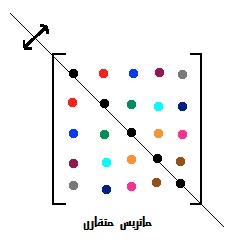
مثال ۱. کدام یک از ماتریسهای زیر متقارن هستند.
۱. $ A = \begin{bmatrix} 1 & 2 & 3 \\ 2 & 0 & 1 \\ 3 & 1 & 5 \end{bmatrix} $
ماتریس A متقارن است، زیرا در آن درایهها نسبت به قطر اصلی متقارن میباشند.
۲. $ B = \begin{bmatrix} 5 & 3 & 0 \\ i & 0 & 1 \\ 0 & 1 & 0 \end{bmatrix} $
ماتریس B متقارن نیست، زیرا در آن درایهها نسبت به قطر اصلی متقارن نمیباشند.
مثال ۲. به ازای چه مقادیری از x و y ماتریس زیر متقارن است؟
$ A = \begin{bmatrix} 5 & 2 & 1 \\ x+y & 0 & 1 \\ y-x & 1 & 5 \end{bmatrix} $
چون ماتریس A متقارن میباشد، در اینصورت درایههای این ماتریس باید نسبت به قطر اصلی متقارن باشند. پس با توجه به این موضوع که $ x+y = 2 , y-x =1$ لذا داریم:
⇒ $ x+y = 2 \rightarrow x = 2 - y $
⇒ $ y = x+1 \rightarrow y = 2-y+1 \rightarrow 2y = 3 \rightarrow y = \frac{3}{2} \rightarrow x = - \frac{1}{2} $
تمرین ۱. به ازای چه مقادری از $ x,y,z $ ماتریسهای زیر متقارن خواهند بود؟
۱. $ A = \begin{bmatrix} 1 & 5 & x+y \\ z & 2 & y \\ 1 & x & 0 \end{bmatrix} $
۲. $ B= \begin{bmatrix} 0 & 5 & 0 \\ x+y & 1 & 2 \\ 0 & 2x+y & 3 \end{bmatrix} $
۳. $ C = \begin{bmatrix} 5 & 2x+z & y \\ 1 & 0 & 1 \\ i & 2z & 0 \end{bmatrix} $
- بازدید: 16185
ویژگی ماتریسهای متقارن
ویژگی ماتریسهای متقارن: در این مطلب سعی داریم، ویژگیهایی را که بر روی ماتریسهای متقارن صدق میکنند، را بیان کنیم.
ویژگی ۱. فرض کنید که $A$ و $B$ دو ماتریس مربعی و متقارن باشند. در اینصورت $ A+B $ متقارن خواهد بود.
زیرا با توجه به ویژگیهایی که برای ترانهاده یک ماتریس و ماتریسهای متقارن $A$ و $B$ گفته شد، داریم:
$ (A+B)^{T} = A^{T} + B^{T} = A + B $
مثال ۱- فرض کنید که دو ماتریس متقارن $A$ و $B$ به صورت زیر بیان شده باشند.
$ A = \begin{bmatrix} 1 & 5 \\ 0 & 2 \end{bmatrix} $
$ B = \begin{bmatrix} i & o \\ 0 & i \end{bmatrix} $
در اینصورت $ A + B $ متقارن نخواهد شد. زیرا با توجه به ویژگی ۱، برای اینکه مجموع دو ماتریس متقارن باشد، باید هر دو ماتریس $A$ و $B$ متقارن باشند که در این مجموع، $B$ متقارن نیست.
ویژگی ۲. اگر A ماتریس مربعی و متقارن باشد. در اینصورت $ \lambda A $ نیز برای اسکالر $ \lambda $ متقارن خواهد شد.
تمرین ۱. فرض کنید که $ A = \begin{bmatrix} 1 & 2 & 3 \\ 2 & 0 & 5 \\ 3 & 5 & 1 \end{bmatrix} $ و $ \lambda = i $ باشد. در اینصورت آیا $ \lambda A $ متقارن است؟
ویژگی ۳. فرض کنید که $A$ و $B$ دو ماتریس متقارن باشند. در اینصورت $ AB $ در حالت کلی متقارن نخواهد بود. برای اینکه دو ماتریس $ AB $ متقارن باشند، حتما باید این دو ماتریس تعویض پذیر باشند. با توجه به ویژگیهای ترانهاده یک ماتریس داریم:
$ (AB)^{T} = B^{T} A^{T} $
حال چون $A$ و $B$ متقارن هستند، لذا $ A^{T} = A $ ،$ B^{T} = B $ و اینکه $ AB = BA $ است. پس داریم:
$ B^{T} A^{T} = BA = AB $
مثال ۲. فرض کنید دو ماتریس $A$ و $B$ به صورت زیر بیان شده باشند. نشان دهید که $ AB $ لزوما متقارن نیست.
فرض کنید که دو ماتریس A و B را به صورت زیر تعریف کرده باشیم:
$ A = \begin{bmatrix} 1 & 2 \\ 2 & 5 \end{bmatrix} $
$ B = \begin{bmatrix} 0 & 3 \\ 3 & 0 \end{bmatrix} $
در اینصورت داریم:
⇒ $ AB = \begin{bmatrix} 1 & 2 \\ 2 & 5 \end{bmatrix} \begin{bmatrix} 0 & 3 \\ 3 & 0 \end{bmatrix} = \begin{bmatrix} 6 & 3 \\ 15 & 6 \end{bmatrix} $
⇒ $ BA = \begin{bmatrix} 0 & 3 \\ 3 & 0 \end{bmatrix} \begin{bmatrix} 1 & 2 \\ 2 & 5 \end{bmatrix} = \begin{bmatrix} 6 & 15 \\ 3 & 6 \end{bmatrix} $
پس در نتیجه $ AB \neq BA $ میباشد.
ویژگی ۴. فرض کنید که A یک ماتریس متقارن باشد. در اینصورت هر توانی از ماتریس A هم متقارن خواهد شد. یعنی داریم:
$ \forall n \in N (A^{n})^{T} = (A^{T})^{n} = A^{n} $
ویژگی ۵. فرض کنید که $A$ یک ماتریس متقارن باشد، هرگاه $ f(x) $ یک تابع چندجملهای به شکل زیر باشد:
$ f(x) = a_{n} x^{n} + a_{n-1} x^{n-1} + ... + a_0 $
در اینصورت $ f(A) $ هم یک ماتریس متقارن خواهد بود.
مثال ۳. فرض کنید که $ A = \begin{bmatrix} 1 & 5 \\ 5 & 0 \end{bmatrix} $ یک ماتریس متقارن باشد. همچنین تابع $ f(x) = x^2 + x $ را در نظر بگیرید. نشان دهید که $ f(A) $ هم متقارن است.
$ f(A) = A^2+A = \begin{bmatrix} 1 & 5 \\ 5 & 0 \end{bmatrix} \begin{bmatrix} 1 & 5 \\ 5 & 0 \end{bmatrix} + \begin{bmatrix} 1 & 5 \\ 5 & 0 \end{bmatrix} = \begin{bmatrix} 26 & 5 \\ 5 & 25 \end{bmatrix} + \begin{bmatrix} 1 & 5 \\ 5 & 0 \end{bmatrix} = \begin{bmatrix} 27 & 10 \\ 10 & 25 \end{bmatrix} $
با توجه به تعریف ماتریسهای متقارن میبینیم که ماتریس حاصل شده نسبت به قطر اصلی متقارن میباشند.
تمرین ۲. فرض کنید که A یک ماتریس مربعی باشد. آیا ماتریس $ AA^{T} $ متقارن است؟
تمرین ۳. فرض کنید که A و B ماتریسهای مربعی باشند. آیا ماتریس $ AB^{T} - BA^{T} $ متقارن است؟
تمرین ۴. فرض کنید که A و B ماتریسهای مربعی باشند. آیا ماتریس $ AB^{T} + B^{T}A $ متقارن است؟
تمرین ۵. فرض کنید که $ A = \begin{bmatrix} 1 & 5 & 7 \\ 5 & 0 & i \\ 7 & i & i \end{bmatrix} $ باشد. نشان دهید که $ f(A) $ با تابع چندجملهای به صورت زیر یک ماتریس متقارن است.
$ f(x) = x^3 + ix $
- بازدید: 4362
ماتریس پاد متقارن
تعریف ماتریس پاد متقارن: فرض کنید که $ A $ یک ماتریس مربعی از مرتبه $ n \times n $ باشد. ماتریس $ A $ را پاد متقارن (یا متقارن کج) گویند، هرگاه داشته باشیم:
$ A^{T} = -A $
در واقع این موضوع بیان میکند که رابطه زیر بین درایههای ماتریس پاد متقارن A برقرار است:
- بازدید: 13906